Why does topology rarely come up outside of topology?

Question

I am currently taking topology and it seems like a completely different branch of math than anything else I have encountered previously.

I find it a little strange that things are not defined more concretely. For example, a topological space is defined as a set $X$ with a collection of open sets $\tau$ satisfying some properties such as the empty set and $X$ are in $\tau$, intersection of two open sets are in $\tau$, and unions of open sets is in $\tau$.

So, it seems that a lot of things are topological spaces, such as the real line equipped with a collection of open sets. But I have not seen anyone bringing this up in other areas of mathematics such as linear algebra, calculus, differential equations or analysis or complex analysis. Sure, open sets and closed sets are brought up but the concept of "topology", "base", etc. etc. are missing entirely.

As you scratch the surface a little more you encounter things such as the subspace topology, product topology, order topology and open sets are defined differently with respect to each of them. But nonetheless outside of a course in topology, you never encounter these concepts.

Is there a reason why topology is not essential for other courses that I have mentioned? Is there a good reference that meshes serious topology (as in Munkres) with more applied area of mathematics?

Answer 1

In 1830 Jacobi wrote a letter to Legendre after the death of Fourier (for an account, see Fourier, Legendre and Jacobi, Kahane, 2011). In it he writes about "L'honneur de l’esprit humain" (The honour of the human mind), which later became a motto for pure mathematics, and the title of a fabulous book by Dieudonné. The translation of the quote exists under different forms, I chose:

Mathematics exists solely for the honour of the human mind.

Which does not prevent unforeseen practical uses of abstract theories: group derivations inspired from polynomial root solving had unexpected everyday-life applications in chemistry and cryptography.

Since you have high expectations about topology, you ought to have a look at a recent application of analysis situs to the world of digital data processing, named Topological data analysis (TDA), driven by people like G. Carlsson (not forgetting people like Edelsbrunner, Frosini, Ghrist, Robins), even in an industrial way (e.g. with Ayasdi company). In a few words, it may extract barcodes from point clouds, based on the concept of persistent homology.

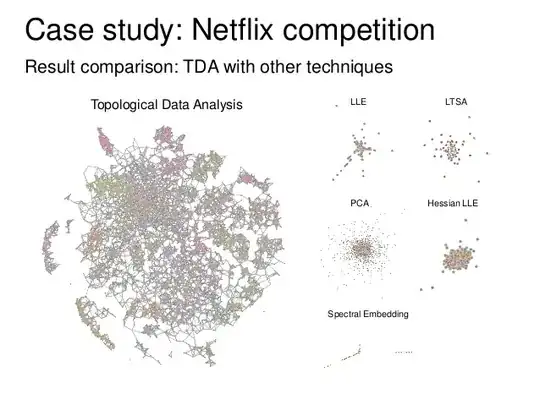
EDIT: on request, I am adding a few relevant links (not advertising)

• Barcodes: The Persistent Topology Of Data, Robert Ghrist, 2008
• Topological Data Analysis, Afra Zomorodian, 2011
• Persistent Homology: Theory and Practice, Herbert Edelsbrunner and Dmitriy Morozov, 2012
• A Short Course in Computational Geometry and Topology, Herbert Edelsbrunner, 2014
• Elementary Applied Topology, Robert Ghist, 2014
• Persistence Theory: From Quiver Representations to Data Analysis, Steve Y. Oudot, 2015
• The site Applied Topology - Qualitative data analysis with a set of preprints

Those methods could be overrated (in practice) yet, from my data processing point of view, topology is pervasive in many applied fields, even when not directly mentioned. Most of the groundbreaking works in signal processing, image analysis, machine learning and data science performed in the past years rely on optimization and convergence proofs, with different norms, pseudo-norms, quasi-norms, divergences... hence topology, somewhat.

Regarding sampling and sensor networks, let me add the presentation Sensors, sampling, and scale selection: a homological approach by Don Sheehy, with slides and abstract:

In their seminal work on homological sensor networks, de Silva and Ghrist showed the surprising fact that its possible to certify the coverage of a coordinate free sensor network even with very minimal knowledge of the space to be covered. We give a new, simpler proof of the de Silva-Ghrist Topological Coverage Criterion that eliminates any assumptions about the smoothness of the boundary of the underlying space, allowing the results to be applied to much more general problems. The new proof factors the geometric, topological, and combinatorial aspects of this approach. This factoring reveals an interesting new connection between the topological coverage condition and the notion of weak feature size in geometric sampling theory. We then apply this connection to the problem of showing that for a given scale, if one knows the number of connected components and the distance to the boundary, one can also infer the higher betti numbers or provide strong evidence that more samples are needed. This is in contrast to previous work which merely assumed a good sample and gives no guarantees if the sampling condition is not met.

Answer 2

One of the basic lessons of 20th century mathematics was that infinite structures are usually best thought of as having a topology (or something like a topology to serve similar purposes). The idea is that everything is a "space" of some sort and not only a set. A pure set with no topological structure is included in this view as the extreme case of the discrete topology.

In that mentality, the question would be reversed: "where does topology not appear"? The list would be quite limited.

The idea of everything being topological is not something that is readily inferred from classes and textbooks. It nevertheless has been the reigning idea in pure mathematics for quite a few decades. Not in applied mathematics (so far).

Only with some finite structures does topology become irrelevant, and not in all of those cases.

"things are not defined more concretely. For example, a topological space is defined as a set with a collection of open sets satisfying some properties"

Topology came out of concrete geometric problems such as counting the "holes" in a surface. It was realized that everything could be formalized in terms of continuous functions, and the open sets definition comes from the epsilon-delta definition of continuity.

subspace topology, product topology, order topology

Given the ubiquity of topology these are only basic vocabulary to describe more substantial things, much like the language of sets, functions and relations.

Answer 3

One subject which relies heavily on topology is functional analysis, you should take a look at that. In basic math courses one does not encounter anything that behaves that wierd , which makes it harder to see the point or "idea" of topology. Taking a serious course in functional analysis will probably be the first place where one encounters structures where things get tricky and one really needs to be familiar with the non-intuitive notions from topology. There are of course a lot of other places where topology is needed but my opinion is that functional analysis is one of the more basic ones and one which is rather easy to understand with limited prior exprience.

https://en.wikipedia.org/wiki/Functional_analysis

Answer 4

In most branches of mathematics that work with topological spaces, most of the spaces people use have only one natural topology* that the people want to work with, and so general discussions of abstract topology are unnecessary. Anywhere you have a metric space, you have a topology, and there are topological questions to ask, but these questions tend to take a back seat to the subject matter. You may care that a space is compact, but only because that lets you prove the things you really want to prove.

I would like to counter your statement that topology isn't important in calculus. The discussion of continuous functions depends intimately on topology, and while most of differential calculus deals with differentiable functions, there are at least two big things in calculus that get used repeatedly that are topological in nature: the extreme value theorem (a statement about compactness of finite closed intervals) and the intermediate value theorem (a statement about how $\mathbb R$ is connected). While the focus of a first semester calculus course will not be on these, they form the theoretical underpinnings for why you know certain problems even have solutions, which is why you can then use calculus to find them.

*As mentioned by another answer, functional analysis is an exception. Given an infinite dimensional space of linear functions, there are usually multiple natural yet distinct ways of putting a topology on the linear dual, and so discussions of topology become important.

Answer 5

A major topic of classical analysis is Fourier series and Fourier integrals. These ideas generalize to analysis on (locally compact) topological groups. A topological group is a group $G$ in which group multiplication $G \times G \rightarrow G$ where $(g,h) \mapsto gh$ and group inversion $G \rightarrow G$ where $g \mapsto g^{-1}$ are both continuous (using the product topology on $G \times G$ in order to speak about a function on it being continuous). Analysis on topological groups is a major theme within representation theory. You might have heard about Fourier series in an undergraduate analysis class, but such a course would not have discussed the Fourier transform on topological groups because the audience wouldn't have the experience to appreciate such a generalization yet. It would look "too abstract."

In addition to topological groups there are topological vector spaces: vector spaces $V$ (over the real numbers, say) in which vector addition $V \times V \rightarrow V$ where $(v,w) \mapsto v+w$ and scalar multiplication $\mathbf R \times V \rightarrow V$ where $(c,v) \mapsto cv$ are continuous, using the product topology on both $V \times V$ and $\mathbf R \times V$ in order to speak about functions on them being continuous. A special feature of finite-dimensional real vector spaces like $V = \mathbf R^n$ is that the usual topology on them is the only topology they have that makes them Hausdorff topological vector spaces. (What about the discrete topology on $\mathbf R^n$? Vector addition on $\mathbf R^n$ is continuous when $\mathbf R^n$ has the discrete topology, but scalar multiplication $\mathbf R \times \mathbf R^n \rightarrow \mathbf R^n$ when $\mathbf R^n$ has the discrete topology and the scalars $\mathbf R$ have their usual topology is not continuous.) That $\mathbf R^n$ has only one Hausdorff topological vector space structure is in some sense why we can talk about concepts like continuity in multivariable calculus without having to get into a treatment of topology first: the usual way we think about continuity of functions on $\mathbf R^n$ is the only reasonable way to do so. However, once you pass to infinite-dimensional spaces the situation changes: these spaces can be made into topological vector spaces in more than one interesting way, and this quickly leads into the area of functional analysis, which is not something you would have seen yet just because you can't learn everything in your first two years of college. Functional analysis is not just abstraction for the sake of pure math: it's the mathematical foundation of quantum physics.

The language of topology is relevant to areas of math that at first glance seem to be unrelated to issues of continuity, such as number theory. The study of solutions to congruences mod $m$ can be reduced to the case that $m = p^k$ is a power of a prime number $p$, and the best way to think systematically about congruences modulo prime powers uses the $p$-adic integers $\mathbf Z_p$ (a compact ring) and the $p$-adic numbers $\mathbf Q_p$ (a locally compact field). A buzzword to look up in this context is "Hensel's lemma," which is the $p$-adic analogue of Newton's method from classical analysis. The $p$-adic numbers were created by Hensel at the end of the 19th century, but the original description of his ideas were muddled and awkward because he lacked the topological language that greatly simplifies what is going on (once you are used to the language so that you can recognize certain topological features of the situation). If you've never heard of $p$-adic numbers, to convey their importance I'll just point out that the solution to Fermat's Last Theorem depends on them: the work by Wiles is concerned with representations of Galois groups into $p$-adic matrix groups.

The construction of $p$-adic numbers can be extended to the notion of an inverse limit, leading to constructions such as profinite groups (an inverse limit of finite groups). To work with inverse limits you need the language of topology that you think is not used elsewhere but really is: product topology, subspace topology, and base.

Answer 6

The obvious answer is that is often comes up outside topology.

But I have not seen anyone bringing this up in other areas of mathematics such as linear algebra, calculus, differential equations or analysis or complex analysis.

You haven't seen any topology in these classes? Point set topology is simply an extension of analysis from metric spaces to topological spaces. In your analysis class you absolutely must have covered connectedness, compactness, open/closed sets.

As you scratch the surface a little more you encounter things such as the subspace topology, product topology, order topology and open sets are defined differently with respect to each of them.

Subspace topology doesn't come up? How can you possibly consider functions on $[0,1]$ instead of $\Bbb{R}$ then?

Product topology doesn't come up? You've done multivariable calculus haven't you?

Order topology doesn't come up? This is THE topology on $\Bbb{R}$, on which all of calculus and undergrad real analysis is done.

You really have been doing topology the ENTIRE time. Now you're just calling it what it is. The reason why you didn't see the word "topology" before is simply because it isn't necessary. However in further classes such as functional analysis, it will be necessary to discuss different topologies and be precise.

Answer 7

An elegant theorem of Brouwer's asserts that a continuous map from a disk to itself necessarily has a fixed point. Probably the most accessible proof of this is an algebraic-topology proof using a relative homology group. That's an example to illustrate that the assumption of your question is not correct. This type of fixed point theorem is an indispensable tool in many areas such as geometry and analysis.