Describe the rational points on $3x^2 + y^2 = 4$

Question

Apart from $(x, y) = (0, 2)$ and $(1, 1)$, are there any nonzero rational points on the curve $3x^2 + y^2 = 4$ ?

Answer 1

Let $y=mx+2$ be the equation of a line with rational slope $m$. It intersects the ellipse $3x^2+y^2=4$ at the rational point $(0,2)$. Consequently it's other point of intersection will also be rational.

Conversely, if $(a,b)\not=(0,\pm2)$ is a rational point on the ellipse, the line between it and $(0,2)$ has rational slope $m=(b-2)/a$. (You can even allow $(a,b)=(0,-2)$ if you think of the vertical line $x=0$ as having "rational slope $\pm\infty$.")

Answer 2

Yes, for instance, $(\frac87,\frac27)$.

Here’s the general principle: if a conic has one rational point $P$, you can look at the pencil of lines through $P$ and see where each intersects your curve. A conic over $\Bbb Q$ and a line defined over $\Bbb Q$ have two points in common always, and either they consist of a pair of $\Bbb Q$-conjugate points or they both are rational. Since $P$ is rational, the other is too. Now to work it out:

Take your point $P$ to be $(0,-2)$, and look at the line of slope $m$ passing through $P$, namely $Y=mX-2$, and intersect with your curve $3X^2+Y^2=4$: \begin{align} 3X^2 + (mX-2)^2&=4\\ 3X^2+m^2X^2-4mX&=0\\ (m^2+3)X^2&=4mX\quad\text{(exclude $X=0$)}\\ X&=\frac{4m}{m^2+3}\\ Y&=m\frac{4m}{m^2+3}-2=\frac{2m^2-6}{m^2+3}\,, \end{align} and any rational value of $m$ gives you a rational point on your curve. I took $m=2$ to get the point I quoted above.

Answer 3

Yes. Here's a way to construct some: take any prime $p\equiv1\pmod3$ and write it in the form $a^2+3b^2$ (this is always possible, see below). Then a case of the generalized Brahmagupta-Fibonacci-identity gives $$p^2=3\cdot(2ab)^2+(a^2-3b^2)^2$$ $$4p^2=3\cdot(a^2+2ab-3b^2)^2+(a^2-6ab-3b^2)^2,$$

so a possible non-trivial solution is $$3\left(\frac{a^2+2ab-3b^2}{a^2+3b^2}\right)^2+\left(\frac{a^2-6ab-3b^2}{a^2+3b^2}\right)^2=4.$$

In fact, the above formula gives you an entire family of solutions, just pick any $a,b\in\Bbb Z\;$! It's nice though to see some number theory telling what kind of solutions we may expect to come out of that formula.

Example. $37\equiv1\pmod3$. We find $37=5^2+3\cdot2^2$, so one solution is

$$3\left(\frac{5^2+20-3\cdot2^2}{37}\right)^2+\left(\frac{5^2-60-3\cdot2^2}{37}\right)^2=4,$$ that is, $$3\cdot\left(\frac{33}{37}\right)^2+\left(\frac{-47}{37}\right)^2=4$$ (And you can ignore the minus sign, of course.)

In fact we have:

Theorem. $n\in\mathbb N$ is of the form $a^2+3b^2$ iff every prime divisor $p\equiv2\pmod3$ of $n$ comes with even exponent in the factorisation of $n$.

(For the hardest direction, see the beautiful descent proof at Let $p$ be prime and $(\frac{-3}p)=1$. Prove that $p$ is of the form $p=a^2+3b^2$.)
What's most interesting here is that there's also a way to construct non-trivial solutions, the so-called generalized Brahmagupta-Fibonacci-identity: $$\left(a^2 + 3b^2\right)\left(c^2 + 3d^2\right) = \left(ac-3bd\right)^2 + 3\left(ad+bc\right)^2.$$

Let $n\in\Bbb N$ be an integer that is non-trivially representable as $a^2+3b^2$. Then the above identity gives $$n^2=(a^2-3b^2)^2+3\cdot(2ab)^2$$ $$4n^2=(a^2-6ab-3b^2)^2+3\cdot(a^2+2ab-3b^2),$$ so we've got a rational solution to $3x^2+y^2=4$.

Of course, we could also simply have taken $4n^2=(2a^2-6b^2)^2+3\cdot(4ab)^2$, but as you can see the Brahmagupta-identity gives more possibilities.

Answer 4

Let's just give the final result for @Barry Cipra:'s answer:

Taking the line $y = - m x + 2$ passing through the point $(0,2)$ of the curve, the other intersection point with the curve is \begin{eqnarray} x &= &\frac{4 m}{3 + m^2} \\ y &= & \frac{ 2 ( 3 - m^2)}{3+m^2} \end{eqnarray}

Answer 5

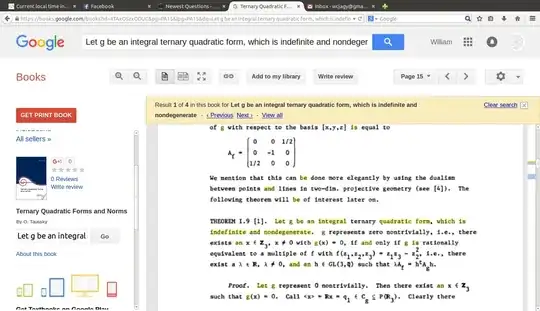
There is a viewpoint initiated in Fricke and Klein (1897), especially pages 507-508, and reported in Theorem I.9 on page 15 of PLESKEN. It is rigid as to dimensions: given an isotropic (over $\mathbb Q$ and therefore $\mathbb Z$) ternary quadratic form, it parametrizes all integer primitive solutions by one or more triples of binary quadratic forms.

The outcome is that every primitive integer solution to $$ 3x^2 + y^2 = 4 z^2 $$ can be written with $\gcd(u,v) = 1$ and $u \neq v \pmod 3$ as $$ x = u^2 + 2 u v, \; \; y = -u^2 + 2 u v + 2 v^2, \; \; z = u^2 + uv + v^2. $$ Here $z > 0,$ we may choose $\pm x$ but we do not get to choose the sign of $y.$

For your other question, you want $x/z = (s/t)^n$ for $n \geq 3.$ My first impression is that this means $$ u^2 + 2 u v = s^n, \; \; \; u^2 + u v + v^2 = t^n. $$ Either one can be accomplished alone, I don't see doing them simultaneously.

For the curious, the matrix identity guaranteed by the theorem in Plesken is $$ \left( \begin{array}{rrr} 1 & -1 & 1 \\ 2 & 2 & 1 \\ 0 & 2 & 1 \end{array} \right) \left( \begin{array}{rrr} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -4 \end{array} \right) \left( \begin{array}{rrr} 1 & 2 & 0 \\ -1 & 2 & 2 \\ 1 & 1 & 1 \end{array} \right) = -12 \left( \begin{array}{rrr} 0 & 0 & \frac{1}{2} \\ 0 & -1 & 0 \\ \frac{1}{2} & 0 & 0 \end{array} \right) $$

Answer 6

Let's solve $x^2+3y^2=4z^2$ in integers. Let wlog $\gcd(y,z)=\gcd(z,x)=1$.

If $\gcd(x,y)=2$, then let $x=2x_1$, $y=2y_1$. Then $x_1^2+3y_1^2=z^2$, so $3y_1^2=(z+x_1)(z-x_1)$, so $\gcd(z+x_1,z-x_1)=1$, so two cases:

$1)\ $ $z+x_1=\pm 3a^2$, $z-x_1=\pm b^2$. Then $x_1=\pm \frac{3a^2-b^2}{2}$, $z=\pm\frac{3a^2+b^2}{2}$, so $y=\pm 2ab$.

$2)\ $ $z+x_1=\pm b^2$, $z-x_1=\pm 3a^2$. Then $x_1=\pm\frac{b^2-3a^2}{2}$, $z=\pm \frac{3a^2+b^2}{2}$, so $y=\pm 2ab$.

So if $\gcd(x,y)=2$, then all the solutions are given by $(x,y,z)=\left(\pm \left(b^2-3a^2\right), \pm 2ab, \pm\frac{3a^2+b^2}{2}\right)$ with $a,b\in\mathbb Z$, $a\equiv b\pmod{2}$.

If $\gcd(x,y)=1$, then $3y^2=(2z-x)(2z+x)$ and $\gcd(2z-x,2z+x)=1$. Two cases:

$1)\ $ $2z-x=\pm 3a^2$, $2z+x=\pm b^2$. Then $x=\pm\frac{b^2-3a^2}{2}$, $z=\pm \frac{b^2+3a^2}{4}$, so $y=\pm ab$.

$2)\ $ $2z-x=\pm b^2$, $2z+x=\pm 3a^2$. Then $x=\pm \frac{3a^2-b^2}{2}$, $z=\pm \frac{b^2+3a^2}{4}$, so $y=\pm ab$.

So if $\gcd(x,y)=1$, all the solutions are given by $(x,y,z)=\left(\pm\frac{b^2-3a^2}{2},\pm ab,\pm \frac{b^2+3a^2}{4}\right)$ with $a,b\in\mathbb Z$, $a\equiv b\pmod{2}$.

If $x^2+3y^2=4$ for rational $x,y$, then let $(x,y)=(p/q,r/s)$ with $p,q,r,s\in\mathbb Z$, $qs\neq 0$.

Then $p^2+3r^2=4(qs)^2$, so either $(p,r,qs)=\left(\pm \left(b^2-3a^2\right), \pm ab, \pm\frac{3a^2+b^2}{2}\right)$ or $(p,r,qs)=\left(\pm\frac{b^2-3a^2}{2},\pm ab,\pm \frac{b^2+3a^2}{4}\right)$ with $a,b\in\mathbb Z$, $a\equiv b\pmod{2}$, $a,b$ not both $0$.

$(x,y)=\left(\pm\frac{b^2-3a^2}{2q},\pm \frac{b^2+3a^2}{4s}\right)$ with $qs=\frac{b^2+3a^2}{4}$ and $a,b,q,s\in\mathbb Z$, $a\equiv b\pmod{2}$, $a,b$ not both $0$ classifies all the solutions.