4

Does exist a triangle with sides a integer length where one of height is equal to the side which is the base?

enter image description here

$a,k,l$ -natural, $a$ is lenght of hight

piteer
  • 6,310
  • If there exists then thats a straight line! – Archis Welankar Dec 23 '15 at 15:25
  • The numbers $a,b,c,d$ you gave in $(a,a+b,c)$ and $(b,a+b,d)$ are not in the picture. – Dietrich Burde Dec 23 '15 at 16:00
  • I have tried to solution, but it maby a wrong way. I deleted my try. – piteer Dec 23 '15 at 16:01
  • 1
    I know that: Height determines two right-angled triangles with sides that are integers. – piteer Dec 23 '15 at 16:05
  • An answer by @DietrichBurde was just posted, but I will put a different idea as a comment (didn't check if it would work). The area of the triangle would be $A=a^2/2$ where $a$ is the height, and then also use Heron's formula to try to come up with a contradiction. – Mirko Dec 23 '15 at 16:11
  • @Mirko: I already tried what you suggest, without success. (And I remain unconvinced by Dietrich's answer.) – TonyK Dec 23 '15 at 16:13
  • @TonyK I have to go, but will try to finish the argument later. – Dietrich Burde Dec 23 '15 at 16:27
  • We can assume $a=1$, and then ask: can $l$ and $k$ both be rational? In other words, does there exist $x$ (not necessarily rational) such that $\sqrt{1 + x^2}$ and $\sqrt{1+(1-x)^2}$ are both rational? – TonyK Dec 23 '15 at 16:31
  • In fact, if $r=\sqrt{1+x^2}$ and $s=\sqrt{1+(1-x)^2}$ are both rational, then so is $x=\frac12(1+r^2-s^2)$. So the problem is the same whether or not we require that $x$ be rational. – TonyK Dec 23 '15 at 17:00

2 Answers2

2

In formulas, we want to find positive integers $a,b,c,d$ solving the Diophantine equations $$ a^2+(a+b)^2=c^2 $$

$$ b^2+(a+b)^2=d^2. $$ In particular, we obtain the Diophantine equation $$ a^2+d^2=b^2+c^2, $$ which has been studied [here]( Diophantine equation $a^2+b^2=c^2+d^2$). hence there are integers $p,q,r,s$ such that $$ (a,b,c,d)=(pr+qs,ps+qr,pr-qs,qr-ps). $$ Use this to show that there are no solutions (if I am not wrong); the equations then are given by $$ (2pr + ps + qr)(ps + qr + 2qs) + (pr + qs)^2=0, $$

$$ (pr + 2ps + qs)(pr + 2qr + qs) + (ps + qr)^2=0. $$

Community
  • 1
Dietrich Burde
  • 130,978
  • It's a very hard system for me. – piteer Dec 23 '15 at 16:11
  • I can't see where your Diophantine equations come from. What are $a,b,c,d$ in terms of the OP's diagram? – TonyK Dec 23 '15 at 16:12
  • the link you provide(d) says that the formulas you include(d) in your (original unedited) answer do not generate all solutions (for Pythagorean quadruples) – Mirko Dec 23 '15 at 16:14
  • @TonyK Yes, I took them from his pairs $(a,a+b,c)$ and $(b,a+b,d)$. – Dietrich Burde Dec 23 '15 at 16:14
  • @DietrichBurde How to solve this system? – piteer Dec 23 '15 at 16:22
  • 1
    @DietrichBurde: "I took them from his pairs": Wrongly, I think. But that part looks OK now. However, the question remains: are there any solutions? I don't think you have addressed this at all. – TonyK Dec 23 '15 at 16:23
  • Your answer seems to assume that the height splits the base into two pieces of integer length, and I don't think this is intended in the problem. Please clarify how your answer relates to the question. What are your $a,b,c,d$? The original statement did not have these, an intermittent (and perhaps incorrect) version did (resulting from your request for clarification), but current version (which I think is the intended original version) does not assume the base is split into integer parts. – Mirko Dec 23 '15 at 16:23
  • @Mirko That's what the OP wrote before: integer triples $(a,a+b,c)$ and $(b,a+b,d)$. Now he has edited. – Dietrich Burde Dec 23 '15 at 16:31
  • 1
    @Mirko: I think the mapping from Dietrich's $a,b,c,d$ to maxkor's diagram is clear: Dietrich's $c$ is maxkor's $l$; Dietrich's $d$ is maxkor's $k$; and Dietrich's $a+b$ is maxkor's $a$. The question has bifurcated, in a sense, according as (Dietrich's) $a$ has to be an integer or not. I would be interested in a solution to either of these two questions. – TonyK Dec 23 '15 at 16:41
  • @TonyK I looked up the original statement again, it did have $a,b,c,d$ (which I did not read carefully at the time, I apologize). As I understood the question without reading the $a,b,c,d$, I did not immediately realize that one version of the question (with the $a,b,c,d$) assumed the base is split into integer parts, and another (current, intended?, the first paragraph or the original) version does not make this additional assumption. (That is, the original statement asked two questions, which were supposed to be a restatement of each other, but were not.) – Mirko Dec 23 '15 at 16:48
  • @Mirko: See my comment to the OP $-$ the question of whether the base has to be split into integer parts is irrelevant. – TonyK Dec 23 '15 at 17:01
  • @TonyK Thank you, I just noticed that the question (of whether the base has to be split into integer parts) is irrelevant, as all cosines of the triangle angles must be rational, and hence the base is split into rational pieces https://en.wikipedia.org/wiki/Integer_triangle#Side_split_by_an_altitude Also, Heronian triangles might be related – Mirko Dec 23 '15 at 17:09
0

[Note: This is probably the same as what Dietrich said, only I like to see the geometry.]

The question is equivalent to asking if there is a triangle with rational side lengths, since we can just scale by the product of the denominators and get integers. So we can assume that $a=1$, since we can just scale by the inverse of whatever rational number $a$ is.

Geometrically, this allows us to put our triangle in the $1\times 1$ square in the cooridinate plane. This now only works for triangles with the third vertex between (0,1) and (1,1). I suppose we would need to modify this to use the law of cosines for the rest of the triangles. 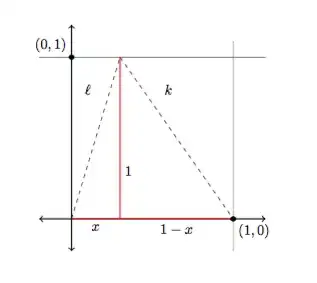Triangle with base on the x-axis and top corner in between (0,1) and (1,1).

Then it is just the pythagorean theorme and we have that $$\ell^2 =x^2+1$$ and $$k^2=(1-x)^2+1. $$

We want $k$ and $\ell$ to be rational, so lets just call $\ell=\frac{p}{q}$. Then $$x^2=\frac{p^2}{q^2}-1= \frac{p^2-q^2}{q^2},$$ thus $$x= \frac{\sqrt{p^2-q^2}}{q}.$$

So with some replacement and simplification, $$k^2=2-2x+x^2$$ $$k^2=2-2\frac{\sqrt{p^2-q^2}}{q}+\frac{p^2-q^2}{q^2}$$ $$k^2=\frac{2q^2}{q^2}-\frac{2q\sqrt{p^2-q^2}}{q^2}+\frac{p^2-q^2}{q^2}$$ $$k^2=\frac{q^2-2q\sqrt{p^2-q^2}+p^2}{q^2}$$ $$k=\frac{\sqrt{q^2+p^2-2q\sqrt{p^2-q^2}}}{q}$$

Then all we need is that the numerator is an integer. I am in the process of making mathematica find one, but I checked the first $1000\times 1000$ pairs of integers for $p<q$ and came up with nothing... Will let you know if I find something though.

Thanks to TonyK for finding a mistake of mine.

Community
  • 1
N. Owad
  • 6,822