What does same algebraic structure mean in group theory and when would two groups have the same algebraic structure? What properties should be checked?
That would be great if you could explain it with some examples of groups with the same structure and groups with different structure.
Compare the addition table mod $4$ and the multiplication table mod $5$ shown below. Ignore the row and the column corresponding to $0$ in the multiplication table mod $5$. You get a multiplicative group mod $5$ that has the same structure of the additive group mod $4$. The tables are the same when you rename the elements as follows: $(0,1,2,3) \to (1,2,4,3)$. It is in this sense that the two groups have the same structure: they are the same when you rename the elements of one group with the elements of the other group. This is called an isomorphism between the two groups.
The Klein four-group is another group with $4$ elements but it is not isomorphic to these ones, because the diagonal is always $1$. They don't have the same structure.
(images courtesy of Wolfram Alpha)
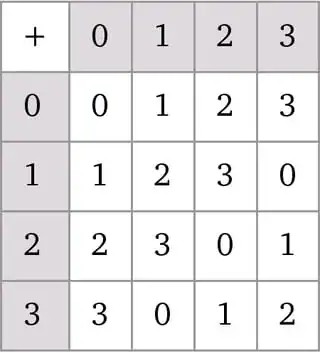
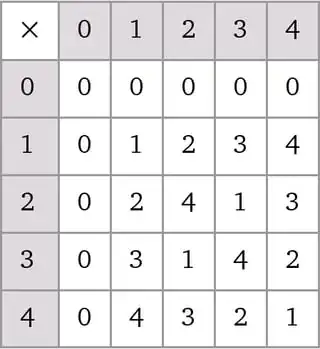
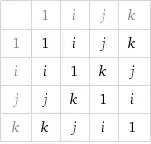
As Crostul said in the comment above basically two groups have the same structure if they are isomorphic.
This notion has meaning for structures of the same type, that is for structures that have operations and relations with the same names.
An isomorphism is basically a bijection between the underlying sets of the algebraic structures considered that preserves the structure: in the case of algebraic structures, where the structure is given by operations, a mapping $f \colon A \to B$ is an isomorphism from the structure $A$ into the structure $B$ if and only if for every operation $\sigma$, of arity $n$, the following holds $$\forall x_1,\dots,x_n \in A\ f(\sigma^A(x_1,\dots,x_n))=\sigma^B(f(x_1),\dots,f(x_n))\ .$$
I denote by $\sigma^A$ the operation $\sigma$ in $A$ and by $\sigma^B$ the corresponding operation in $B$.
To prove that two structure $A$ and $B$ are isomorphic one have to provide a bijective mapping $f \colon A \to B$ that satisfies the condition above for every operation of the underlying structures.
You can think an isomorphism as a dictionary, it renames elements of $A$ with elements of $B$ in such a way that if we perform an operation in $A$ and then translate the result in $B$ or if we first translate the input data and then operate in $B$ we gain the same result.
Examples from the world of groups.
Consider the groups $\mathbb Z/2 \mathbb Z$ and the group of linear applications $\{\text{id},-\text{id}\}$. They are isomorphic via the isomorphism that map $\bar 0$ into $\text{id}$ and $\bar 1$ into $-\text{id}$.
Another example is the group $\mathbb Z$ and the group of integer-translation in $\mathbb R$, they are isomorphic via the map that sends every $n \in \mathbb Z$ into the translation $x \mapsto x+n$.
Of course $\mathbb Z$ and $\mathbb Z/2 \mathbb Z$ aren't isomorphic because there can be no bijection between them, so there can't be any isomorphism either.
The above responses have provided very excellent examples already, as well as describing isomorphisms, so I won't attempt to provide any more.
I will, however, attempt to provide a vastly boiled down "layman's terms" description. When I was a student, I often found these to be helpful to first grasp the general idea, before digging deeper.
Two groups are said to have the same algebraic structure when they are disguised versions of each other.
What do I mean by "disguised"? I mean that
They are exactly the same groups, just with the elements named differently.
Similarly to how $x^2=1$ and $y^2=1$ are exactly the same equations, just labelled differently.
