If you are $N$ radii above a sphere, what fraction of the hemisphere below you can you see?
The answer is so nice that it prompted another question: is there an intuition behind it, in the sense that one might have guessed it before going into the details of the computation? I'll be content with the answer, but I'm really after the intuition, if any springs to mind.
This is essentially a comment to Rahul Narain's answer, about why areas of spherical caps are proportional to the height.
Imagine dropping the sphere into a cylinder into which the sphere fits snugly. Project the sphere onto the cylinder, with parallels of latitude projecting onto circles. This mapping is area-preserving. That can be shown by working with elements $ds$ of length. The same thing was done rigorously by Archimedes about $2200$ years ago, without (explicit) calculus, in On the Sphere and Cylinder.
I take it we're talking about the 2-sphere in 3 dimensions. I'd say this result is only intuitive if your intuition finds it obvious that the surface area of a spherical cap is linearly proportional to its height. Personally, I can't give you you a good intuitive reason why that is true. But taking it as given, you just draw a cross-sectional diagram, find a couple of similar right triangles, and obtain the height of the cap as $1-\frac1N$. The height of the hemisphere is $1$, so that immediately gives you the ratio of their areas.
@André, @Rahul Thanks for the responses. I don't really have any problem with the fact that the area of a spherical cap is proportional to its height; I was wondering if there was an insight that would prompt me to say ``Oh, it's obvious that the rate of change of the height of the cap is proportional to the square of the rate of change of the distance of the observing point to the center of the sphere, since [brilliant insight here].''
While mulling it over for more time than the problem's worth to get a ``no'' answer, I did recall a useful technique that I all too frequently neglect to consider: using circle inversion
Starting with a slice through the observing point, $P$, and the center, $O$, of the sphere we have the left picture below, where the length of the segment $AB$ is the height we want.
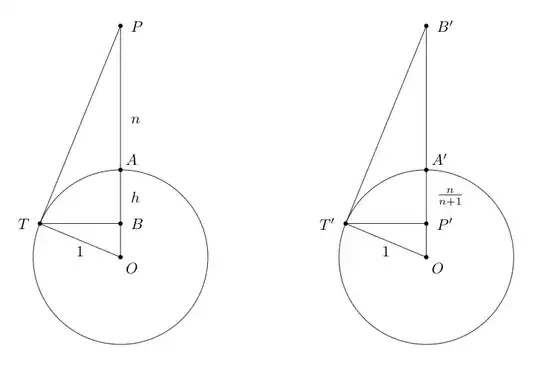Now transform this picture with respect to the reference circle (assumed to be a unit circle) so that a point $X$ of distance $R$ on the ray through the center of the circle is transformed to a point $X'$ on the same ray but with distance $1/R$ from the center. Doing this, we wind up with the picture on the right. While inversion has a lot of interesting properties (not the least of which is the fact that inversion fixes points on the reference circle), the useful property in this situation is that any two points and the origin will form a triangle that is similar to the triangle formed by inverting the two points ($\angle OBT = \angle OT'B'$, for example). This means that the left and right pictures are exactly the same, so a bit of adding and subtracting 1 from various quantities gives us the result that $h=n/(n+1)$, which is exactly the answer we needed.
Whether you find this more or less transparent than other techniques is, of course, up to you, but I thought it was interesting enough to serve as an answer to my own question.