Prove that $e>2$ geometrically.

Question

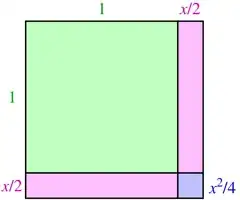
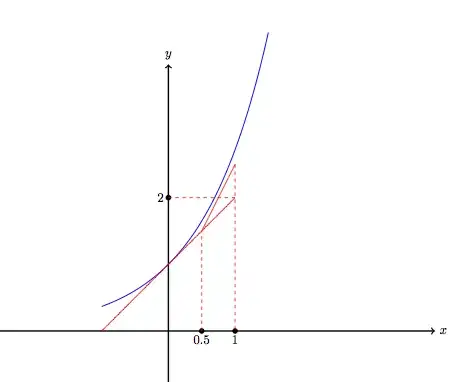
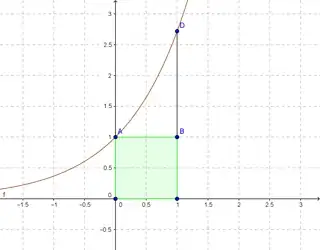
Q: Prove that $e>2$ geometrically.

Attempt: I only know one formal definition of $e$ that is $\lim_\limits{n\to\infty} (1+\frac{1}{n})^n=e$. I could somehow understand that this is somehow related to rotation in the complex plane. $$e^{i\theta}=\cos \theta + i \sin \theta$$ Hence we have $$e^{i\pi}=-1$$ But how can I bring out the value of $e$ when I am showing this rotation in a geometrical figure?

Any hints are appreciated.

EDIT: As per the comments, I am making a small addition to the question which will not affect the existing answers. It is that, as a definition of $e$, one can use any definition which does not use the fact $2<e<3$.

Answer 1

In this image

we see that $$ \color{#00A000}{1}+\color{#C000C0}{x}\le\left(1+\frac x2\right)^2 $$ Therefore, $$ \begin{align} 1+1 &\le\left(1+\frac12\right)^2\\ &\le\left(1+\frac14\right)^4\\ &\le\left(1+\frac18\right)^8\\ &\dots\\ &\le\lim_{n\to\infty}\left(1+\frac1{2^n}\right)^{\large2^n}\\[9pt] &=e \end{align} $$

Answer 2

A better (or at least alternative) definition of $e$ is this:

Let $$ L(x) = \int_1^x \frac{1}{t} dt $$ $L$ is well-defined for positive $x$ by the fundamental theorem of calculus.

With a little work, you can show that $L$ is surjective onto $R$, and since it's clearly increasing and continuous, it's also injective. So it has an inverse, $E$. $L$ is usually known as $\ln$ and $E$ is known as $\exp$.

Then $e = E(1)$ defines a new constant, called Euler's constant.

To show $e > 2$, you need only show that $L(2) < 1$. You can do this by computing an upper bound for the integral that is $L(2)$, i.e $\int_1^2 \frac{1}{t} dt$, using the partition $1, 1.5, 2$; and the left-hand ends as sample points (because $y = 1/x$ is a decreasing functions. The upper integral is then $$ \frac{1}{2} \cdot 1 + \frac{1}{2} \cdot \frac{2}{3} = \frac{5}{6} < 1, $$ and you are done, because the integral is no larger than any of its upper integrals.

Answer 3

A simple geometrical representation can be given noting that $e=f(1)$ for a function $f(x)$ such that $f'(x)=f(x)$ and $f(0)=1$ (This can be a definition of $e$ derived from the definition of the exponential function as the function that represents an exponential growth).

So, representing a graphical approximation of the function (a representation of the Euler Method), as in the figure, We can see that $f(1)=e>2$

Answer 4

You can give a (hyper)geometical interpretation to the inequality

$$(1+x)^n\gt 1+nx\quad\text{when }n\ge2$$

by viewing the left hand side as the volume of an $n$-dimensional hypercube with sides of length $1+x$ and the right hand side as the sum of the volumes of the unit hypercube and the $n$ hyperrectangles of size $1\times1\times\cdots\times1\times x$. Plugging in $x=1/n$ leads to the inequality $e\gt2$.

Answer 5

If $f(x)$ is a convex function, then:

$$f(x + h) \geq f(x) + h f'(x)~\forall x, \forall h > 0. ~~~~~~~~~~~~~~~~(1)$$

---

We know that the function $f(x) = e^x$ has an important geometrical property:

the slope in any point is equal to the function itself

Also, we know that $f(x)$ is positive because of exponentiation. This implies that it is convex, since $f(x)'' = f'(x) = f(x) > 0$ (thanks to A.S. for this point).

Then, (1) holds for $f(x) = e^x$. That is:

$$f(x + h) \geq f(x) + h f'(x)~\forall x, \forall h > 0 \Rightarrow \\ f(x + h) \geq (1+h)f(x)~\forall x, \forall h > 0.$$

If we choose $x=h=1$, then:

$$f(2) \geq 2f(1) \Rightarrow \\ e^2 \geq 2e \Rightarrow \\ e \geq 2.$$

Answer 6

You could use the fact that $e^x$ is its derivative: $$ \int\limits_a^b e^x \, dx = e^b - e^a $$ So $$ e - 1 = \int\limits_0^1 e^x dx = \int\limits_0^1 \left(1 + (\underbrace{e^x - 1}_{\ge 0}) \right) dx > \int\limits_0^1 1\, dx = 1 $$ So $e - 1$ can be interpreted as the area beneath the curve $e^x$ from $x = 0$ to $x = 1$. This area can be divided into the area below the constant function $f(x) = 1$ (green square) and some non-zero area which corresponds to the area below the function $g(x) = e^x - 1 \ge 0$ (the area having the points $A$, $B$, $D$).

(Large version)