In dimension $n = 2$, we have
$$ \int_{D_r} e^{-A^2} \, \mu(dA) = \frac{\pi^2}{2}\left( e^{-r^2} - 1 + r^2 + \frac{r^4}{2} \right) I_2, \tag{*} $$
where $I_2$ is the identity matrix in $M_2(\Bbb{R})$.
In particular, the improper integral does not converge.
I have summarized my solution in my blog posting. But here is my idea: Evaluate the integral of the series expansion
$$ \int_{D_r} e^{-A^2} \, \mu(dA) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m!} \int_{D_r} A^{2m} \, \mu(dA). $$
term by term. Writing $A$ as
$$ A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}, $$
notice that each entry of $A^{2m}$ is a homogeneous polynomial of degree $2m$ in variables $a, b, c, d$. With a little bit of observations, we find that
Lemma 1. Let $D$ be any symmetric domain (in the sense that $-D = D$). Then for any $n \geq 0$,
$$ \int_{D} A^{2m} \, \mu(dA) = I_2 \sum_{i+j+2k=m} \binom{2k+2i}{2i}\binom{2k+2j-1}{2j} \int_{D} a^{2i}d^{2j}(bc)^{2k} \, \mu(dA). \tag{1} $$
Here we exploited the convention that $\binom{-1}{0} = 1$.
Sketch of proof. Each entry of $A^{2m}$ admits a combinatorial interpretation in terms of transition path on a 2-state space:
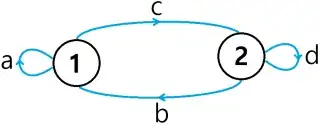
(For example, the path 1→1→1→2→2→2→1→2→1 contributes to the $(1,1)$-entry of $A^8$ with the term $aacddbcb = a^2b^2c^2d^2$.) Also, by the symmetry of $D$, we only need to consider terms with even exponents, i.e., of the form
$$\text{(coef.)}\cdot a^{2i}b^{2j}c^{2k}d^{2l}.$$
These terms correspond to paths where every transition takes place in even numbers. A moment of thought shows that such term corresponds to closed paths. Thus theses term only appear in $(1,1)$-entry and $(2,2)$-entry of $A^{2m}$, and the exponents of $b$ and $c$ are equal. Then $\text{(1)}$ follows by counting the number of such paths. ////
Now, each term in $\text{(1)}$ can be easily computed when $D = D_r$:
Lemma 2. For any $i+j+2k = m$ we have
$$ \int_{D_r} a^{2i}d^{2j}(bc)^{2k} \, \mu(dA) = \frac{(i-\frac{1}{2})!(j-\frac{1}{2})!(k-\frac{1}{2})!^2}{(m+2)!} r^{2m+4}. \tag{2} $$
Of course we are using the convention that $(l-\frac{1}{2})! = \Gamma(l+\frac{1}{2})!$ in $\text{(2)}$. We skip the proof since the proof is easy.
Somewhat surprisingly, the egregious formula $\text{(1)}$ yields simple values:
Lemma 3. For $m \geq 1$ we have
$$ \int_{D_r} A^{2m} \, \mu(dA) = \frac{\pi^2}{2(m+1)(m+2)} r^{2m+4}. $$
(When $m = 0$ we have different value.)
This amounts to prove that
$$ \sum_{i+j+2k=m} \binom{2k+2i}{2i}\binom{2k+2j-1}{2j} (i-\tfrac{1}{2})!(j-\tfrac{1}{2})!(k-\tfrac{1}{2})!^2 = \frac{m! \pi^2}{2}. $$
Proof of this fact can be found in my blog posting. Now assuming that this is true, $\text{(*)}$ easily follows.
