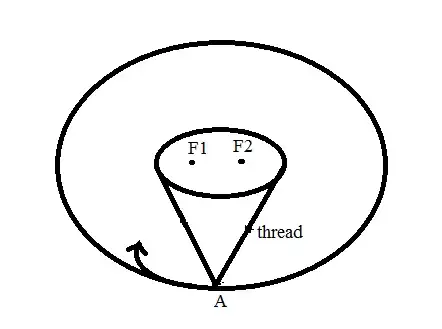
Using a pencil, the thread was pulled on the ellipse. Then the pencil started to rotate around the ellipse. How to prove that the new geometric figure which the pencil drew is also an ellipse (with the same foci as the first ellipse)?
-
I need a Blackboard here for you! :-( – Mikasa Dec 19 '15 at 10:15
-
@Babaxor: i know how to prove that new figure is convex (I haven't possibility to write it in English). But I don't understand how to prove that it is ellipse. – MssExponenta Dec 19 '15 at 10:22
-
I believe the question can be posed this way: Given an ellipse $E$ and distance $d$, show that the locus of points $P$ such that $|\overline{PT}|+|\overline{PU}| = d$ (where $\overleftrightarrow{PT}$ and $\overleftrightarrow{PU}$ are the tangents from $P$ to $E$) is an ellipse with the same foci as $E$. – Blue Dec 19 '15 at 11:32
-
@Blue: That may be what the OP means but that does not come from his wording. The wording seems to mean that given ellipse $E$ and length $e$ that is greater than the circumference of the ellipse, find the locus of points $P$ such that the convex hull formed by $P$ and the ellipse has circumference $e$. This is identical to your formulation only if the arc of the ellipse in the convex hull has constant length, which I doubt to be true. – Rory Daulton Dec 19 '15 at 11:42
-
As Blue and I show, your question is not clear. Please make it more precise. – Rory Daulton Dec 19 '15 at 11:42
-
@Rory Daulton: I add picture. Do I make question understandable? – MssExponenta Dec 19 '15 at 12:21
-
1Yes, the picture makes things much more clear. It looks like a very difficult problem, however. It involves the length of an arc of an ellipse, which I believe is difficult in itself. – Rory Daulton Dec 19 '15 at 12:47
-
See the application of Fagnano's Theorem – Ng Chung Tak Nov 23 '16 at 21:19
1 Answers
Partial answer
Given the two ellipses, we'll check if the thread around the inner ellipse is constant from any point on the outer ellipse.
We can describe the inner and outer ellipses as follows: $$ \begin{align} x &= a \cos(\alpha) && 0<a<e,\ 0<b, \label{1}\tag{1}\\ y &= b \sin(\alpha) && \alpha \in (-\pi, \pi],\ \beta \in (-\pi, \pi]\\ x' &= e \cos(\beta)\\ y' &= \sqrt{e^2-a^2+b^2}\ \sin(\beta) \end{align} $$ The $\sqrt{e^2-a^2+b^2}$ is to make the ellipses have the same foci.
First we want to know where (which two values of $\alpha$) the thread leaves the inner ellipse. We do this by looking which tangent lines of the inner ellipse go through $(x', y')$. The tangent lines can be found by adding a multiple of the derivative: $$ \begin{align} x' &= a \cos(\alpha) + t \cdot (-a\sin(\alpha)) \qquad t \in \mathbb{R} \\ y' &= b \sin(\alpha) + t \cdot (b \cos(\alpha)) \end{align} $$ Let $c = \frac{x'}{a}$ and $d = \frac{y'}{b}$, we have to solve: $$ \begin{align} c &= \cos(\alpha) - t \sin(\alpha)\\ d &= \sin(\alpha) + t \cos(\alpha) \end{align} $$ This seems pretty hard, but using Mathematica we get: $$ \begin{align} m &= d \pm \sqrt{c^2+d^2-1} \label{2}\tag{2} \\ \alpha &= 2 \arctan \left( \displaystyle \frac{m}{c+1} \right) \\ t &= \frac{1-c^2-m^2}{2 m} \end{align} $$ The formula for $\alpha$ is undefined for $c = -1$, but that's no problem, because we'll only check the right part ($\beta \in [-\pi/2, \pi/2]$) of the outer ellipse, which is sufficient because of symmetry. This also prevents us to run into a potential problem with the discontinuity of $\alpha$ and $\beta$ at $\pi$.
We can plug $\alpha$ back in $\eqref{1}$ to find the points on the ellipse: $$ \begin{align} x &= a \cos \left(2 \arctan \left( \frac{m}{c+1} \right) \right) = a \frac{-d m+c+1}{d m+c^2+c} \\ y &= b \sin \left(2 \arctan \left( \frac{m}{c+1} \right) \right) = b \frac{m(c+1)}{d m+c^2+c} \end{align} $$ Now we can make a formula for the length of the thread $L$. In $L_3$ the $\alpha_1$ refers to the lower of the two values of $\alpha$ (choosing $-$ in $\eqref{2}$), and $\alpha_2$ to the higher value (choosing $+$ in $\eqref{2}$). The integrand is the Pythagorean theorem applied to the derivative of $\eqref{1}$. $$ \begin{align} L_1 &= \sqrt{(x' - x_1)^2 + (y' - y_1)^2} \\ L_2 &= \sqrt{(x' - x_2)^2 + (y' - y_2)^2} \\ L_3 &= \int_{\alpha_2}^{\alpha_1+2\pi} \sqrt{a^2 \sin(\alpha)^2 + b^2 \cos(\alpha)^2} \ \mathrm{d}\alpha \\ L &= L_1 + L_2 + L_3 \end{align} $$ The only thing left to do is proving $L$ is constant. We can do this by proving that its derivative to $\beta$ is equal to 0. When writing $L$ as function of $a$, $b$, $e$ and $\beta$, the formula gets pretty big. So you'll want to use a computer for this. We can get rid of the integral in $L_3$ because: $$ \begin{align} \frac{\mathrm{d}L_3}{\mathrm{d}\beta} &= \frac{\mathrm{d}\alpha_1}{\mathrm{d}\beta} \sqrt{a^2 \sin(\alpha_1)^2 + b^2 \cos(\alpha_1)^2} - \frac{\mathrm{d}\alpha_2}{\mathrm{d}\beta} \sqrt{a^2 \sin(\alpha_2)^2 + b^2 \cos(\alpha_2)^2} \end{align} $$ With help of Mathematica we see that $\frac{\mathrm{d}L}{\mathrm{d}\beta}$ is equal to: (Mathematica code)
1/2 ((2 (Sqrt[-a^2 + b^2 + e^2] sinβ + (b^2 (a + e Sqrt[1 - sinβ^2]) (a Sqrt[-a^2 + b^2 + e^2] sinβ - Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))) (Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] - (b^2 e sinβ (a Sqrt[-a^2 + b^2 + e^2] sinβ - Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])) + (b^2 (a + e Sqrt[1 - sinβ^2]) Sqrt[(-1 + sinβ^2)/((a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2)))] (a^4 sinβ + b^2 e^2 sinβ - a^2 (b^2 + e^2) sinβ + a Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])) - (a^2 b^2 (a + e Sqrt[1 - sinβ^2]) (-Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]/ a) (-b^2 e^2 Sqrt[-a^2 + b^2 + e^2] (1 - sinβ^2)^( 3/2) + Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (a^2 b^2 + (2 a^4 + b^2 e^2 - 2 a^2 (b^2 + e^2)) sinβ^2) - b sinβ (a b^2 e + 2 (a^2 - b^2) (a^2 - e^2) Sqrt[ 1 - sinβ^2]) Sqrt[-1 + ((-a^2 + b^2 + e^2) sinβ^2)/b^2 - (e^2 (-1 + sinβ^2))/ a^2]))/(Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))] (b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) - a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[-(a^2 - e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))^2)) + (2 (a + e Sqrt[1 - sinβ^2]) (a^4 sinβ^2 + b^2 e^2 (-1 + sinβ^2) + a sinβ Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)] + a^2 (-e^2 sinβ^2 - b^2 (-1 + sinβ^2))) (-e sinβ + (a^3 (a b^2 - a (-a^2 + b^2 + e^2) sinβ^2 + b^2 e Sqrt[1 - sinβ^2] + sinβ Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]) (-b^2 e^2 Sqrt[-a^2 + b^2 + e^2] (1 - sinβ^2)^(3/2) + Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (a^2 b^2 + (2 a^4 + b^2 e^2 - 2 a^2 (b^2 + e^2)) sinβ^2) - ( sinβ (a b^2 e + 2 (a^2 - b^2) (a^2 - e^2) Sqrt[ 1 - sinβ^2]) Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])/ a))/(Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))] (b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) - a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[-(a^2 - e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))^2) - (a^2 b (-b^2 e^2 Sqrt[-a^2 + b^2 + e^2] (1 - sinβ^2)^(3/2) + Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (a^2 b^2 + (2 a^4 + b^2 e^2 - 2 a^2 (b^2 + e^2)) sinβ^2) + sinβ (b^2 e + 2 a (-a^2 + b^2 + e^2) Sqrt[ 1 - sinβ^2]) Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))/(Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))] (-b^3 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a b sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[-(a^2 - e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])))))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])))/(\[Sqrt](((a + e Sqrt[1 - sinβ^2])^2 (a^4 sinβ^2 + b^2 e^2 (-1 + sinβ^2) + a sinβ Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)] + a^2 (-e^2 sinβ^2 - b^2 (-1 + sinβ^2)))^2)/(b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) - a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))^2 + (Sqrt[-a^2 + b^2 + e^2] sinβ + (b^2 (a + e Sqrt[1 - sinβ^2]) (a Sqrt[-a^2 + b^2 + e^2] sinβ - Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])))^2)) + (-((2 (a + e Sqrt[1 - sinβ^2]) (a^4 sinβ^2 + b^2 e^2 (-1 + sinβ^2) - a sinβ Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)] + a^2 (-e^2 sinβ^2 - b^2 (-1 + sinβ^2))) (-e sinβ - (a^3 (-(( e sinβ)/a) - ( Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]/a))/b^2 - ( sinβ Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (b Sqrt[-a^2 + b^2 + e^2] + ( b (-a^2 + b^2) (a^2 - e^2) sinβ)/( a Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])))/b^3))/(a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2) + ( a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))/ b^2) - (a^3 (a b^2 - a (-a^2 + b^2 + e^2) sinβ^2 + b^2 e Sqrt[1 - sinβ^2] - sinβ Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]) (-b^2 e^2 Sqrt[-a^2 + b^2 + e^2] (1 - sinβ^2)^(3/2) + Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (a^2 b^2 + (2 a^4 + b^2 e^2 - 2 a^2 (b^2 + e^2)) sinβ^2) + ( sinβ (a b^2 e + 2 (a^2 - b^2) (a^2 - e^2) Sqrt[ 1 - sinβ^2]) Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])/ a))/(Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))] (b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[-(a^2 - e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))^2)))/(b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))) + 2 (Sqrt[-a^2 + b^2 + e^2] sinβ + (b^2 (a + e Sqrt[1 - sinβ^2]) (a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ - Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))) (Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] - (b^2 (a + e Sqrt[1 - sinβ^2]) Sqrt[(-1 + sinβ^2)/((a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2)))] (-a^4 sinβ - b^2 e^2 sinβ + a^2 (b^2 + e^2) sinβ + a Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))/(b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])) - (b^2 e sinβ (a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ - Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])) - (a^2 b^2 (a + e Sqrt[1 - sinβ^2]) (Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]/ a) (-b^2 e^2 Sqrt[-a^2 + b^2 + e^2] (1 - sinβ^2)^( 3/2) + Sqrt[(-a^2 + b^2 + e^2) (1 - sinβ^2)] (a^2 b^2 + (2 a^4 + b^2 e^2 - 2 a^2 (b^2 + e^2)) sinβ^2) + b sinβ (a b^2 e + 2 (a^2 - b^2) (a^2 - e^2) Sqrt[ 1 - sinβ^2]) Sqrt[-1 + ((-a^2 + b^2 + e^2) sinβ^2)/b^2 - (e^2 (-1 + sinβ^2))/ a^2]))/(Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))] (b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[-(a^2 - e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))^2)))/(\[Sqrt](((a + e Sqrt[1 - sinβ^2])^2 (a^4 sinβ^2 + b^2 e^2 (-1 + sinβ^2) - a sinβ Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)] + a^2 (-e^2 sinβ^2 - b^2 (-1 + sinβ^2)))^2)/(b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]))^2 + (Sqrt[-a^2 + b^2 + e^2] sinβ + (b^2 (a + e Sqrt[1 - sinβ^2]) (a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))]))/(-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ - Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])))^2)) - (2 a b (a^3 e sinβ + a^4 sinβ Sqrt[1 - sinβ^2] - a^2 (b^2 + e^2) sinβ Sqrt[1 - sinβ^2] + a (-e^3 sinβ + Sqrt[-(a^2 - e^2) (a^2 - b^2 - e^2) (-1 + sinβ^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]) + e (b^2 e sinβ Sqrt[1 - sinβ^2] + Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])) Sqrt[-((( 4 a^2 (-a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[(-a^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])^2)/( b^2 (a + e Sqrt[1 - sinβ^2])^2) + b^2 (-1 + (-a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])^2/( b^2 (a + e Sqrt[1 - sinβ^2])^2))^2)/((a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))))])/((-b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (a^3 sinβ - a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])) Abs[ 1 + (-a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])^2/( b^2 (a + e Sqrt[1 - sinβ^2])^2)]) - (2 a b (-a^3 e sinβ - a^4 sinβ Sqrt[1 - sinβ^2] + a^2 (b^2 + e^2) sinβ Sqrt[1 - sinβ^2] + a (e^3 sinβ + Sqrt[-(a^2 - e^2) (a^2 - b^2 - e^2) (-1 + sinβ^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)]) + e (-b^2 e sinβ Sqrt[1 - sinβ^2] + Sqrt[(-a^2 + e^2) (-a^2 + b^2 + e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])) Sqrt[-((( 4 (a^2 Sqrt[-a^2 + b^2 + e^2] sinβ + a Sqrt[(-a^2 + e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])^2)/( b^2 (a + e Sqrt[1 - sinβ^2])^2) + b^2 (-1 + (a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])^2/( b^2 (a + e Sqrt[1 - sinβ^2])^2))^2)/((a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))))])/((b^2 (a^2 sinβ^2 + a e Sqrt[1 - sinβ^2] - e^2 (-1 + sinβ^2)) + a sinβ (-a^3 sinβ + a e^2 sinβ + Sqrt[(a^2 - e^2) (a^2 - b^2 - e^2) (b^2 + a^2 sinβ^2 - b^2 sinβ^2)])) Abs[ 1 + (a Sqrt[-a^2 + b^2 + e^2] sinβ + Sqrt[-(a^2 - e^2) (a^2 sinβ^2 - b^2 (-1 + sinβ^2))])^2/( b^2 (a + e Sqrt[1 - sinβ^2])^2)]))
Inserting arbitrary values for $a$, $b$, $e$ and $sin\beta$ and calculating it numerically seems to always yield 0. It is left as an exercise for the reader to prove this is true for all $0<a<e, 0<b, -1 \le sin\beta \le 1$.
- 2,795