4

I am an unconditional admirer of WolframAlpha and for this reason I want to let the people of this error (or is it really the fault of mine?). If I'm not mistaken, I would be very happy to contribute, communicating this default calculation, to this extraordinary and beneficial website.

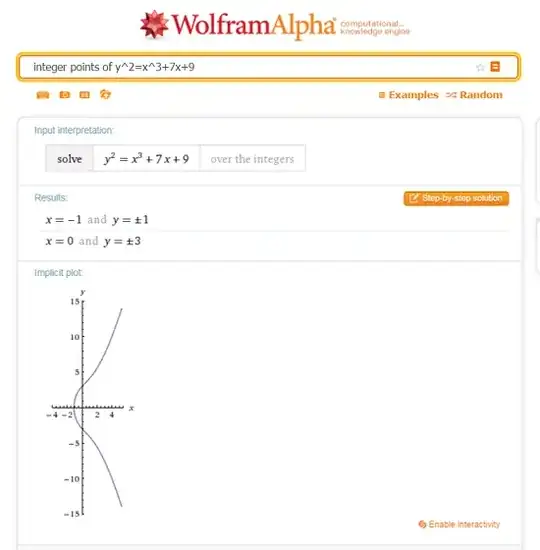
I was watching something on the cubic curve $$y^2=x^3+7x+9$$ More precisely I was interested in integer points $(x, y)$ with both coordinates being prime numbers. I thought having in hand the point $ (5,\pm 13) $ but, consulting WolphramAlpha, his answer gives only the two points $(-1,\pm 1)$ and $(0,\pm 3)$

Maybe I need to rest a bit ...

enter image description here

pjs36
  • 17,979
Piquito
  • 29,594
  • 1
    $5^{2} \ne 13^{3} + 7(13) + 9$..

    Have a rest.

     – Matthew Cassell Dec 19 '15 at 00:34
  • 1
    Perhaps OP meant (5,13) – user217285 Dec 19 '15 at 00:42
  • Absolutely! it is $(5,\pm13)$ – Piquito Dec 19 '15 at 00:46
  • Thank you, @pjs36 for the tag of (computer-algebra-systems) I did not know. – Piquito Dec 19 '15 at 00:56
  • Sure! I'm just trying to get the question visibility; I like it. I have no idea how to get WolframAlpha to find integer points, and I'm interested in finding out. The more I think about it, it might help to attach a concrete question, like "Can I use WolframAlpha to find integer points on an elliptic curve?" or something. I think that's what you're asking, but I'm not sure. – pjs36 Dec 19 '15 at 00:57
  • This is certainly due to excellent programming and powerful computer. The elliptic curves are fascinating but at all times they ask very hard calculations. And their open problems are extremely difficult (there are waiting for a proof the heavenly Birch and Swinnerton-Dyer conjecture and that the rank is not bounded (or find a bound tough i feel rather not bounded) – Piquito Dec 19 '15 at 01:09
  • 2
    For stuff on elliptic curves, the online Magma calculator is a much better choice than wolfram alpha. Throwing following commands Q<x> := PolynomialRing(Rationals());} E00 := EllipticCurve(x^3+7*x+9); Q00 := IntegralPoints(E00); Q00; to the online calculator, one get $(x,y) = (-1,\pm 1), (0, \pm 3), (5, \pm 13), (17, \pm 71), (27,\pm 141)$. – achille hui Dec 19 '15 at 01:24
  • Extremely interesting: the curve has two points both with the two prime-coordinates !. Thank for the Magma calculator but the WolframAlpha will be always interesting. – Piquito Dec 19 '15 at 02:16
  • @achillehui: May I know what is the *Magma* command to find an initial rational point (not necessarily integral) on $x^3+7x+9 = y^2$? – Tito Piezas III Jan 15 '16 at 15:03
  • @TitoPiezasIII I'm not that familiar with Magma but you can use Generators(E00) to get the generators. – achille hui Jan 15 '16 at 15:08
  • @achillehui: Thanks. I'm trying to answer this question. It can be reduced to solving $p^3+q^3 = 313^2$, hence the elliptic curve $w^3-432\cdot313^4 = t^2$. Using your IntegralPoints command, Magma said there is, but it seems too big to print it out. Same with the Generators thingie. :( Do you know how to find a rational point on that elliptic curve? – Tito Piezas III Jan 15 '16 at 15:20
  • @TitoPiezasIII I don't. Actually, I tried using magma a few hours ago for the same EC and have essentially same problem as you. – achille hui Jan 15 '16 at 15:26
  • @achillehui: Ok, thanks though. – Tito Piezas III Jan 15 '16 at 15:30
  • I finally think that Wolfram was not wrong but gave answers ranging over a fixed interval (more so, I think it offers the possibility of extending its considered range) – Piquito Jan 16 '16 at 18:21

1 Answers1

1

I believe wolfram is right, $$(-13)^3+7(-13)+9=-2279 \neq 5^2$$ and similarly $$13^3+7(13)+9=2297 \neq 5^2$$ and $\sqrt{2297} \notin \mathbb Z$

EDIT: Switching $x$ and $y$ it seems that $5^3+7(5)+9=13^2$, so yes you're correct!