1

$$\mathrm{div}\ {\bf F} = \lim_{V\to\{0\}}{1\over|V|}\oint_V {{\bf F}\cdot d{\bf a}}$$

Wikipedia says:

In physical terms, the divergence of a three dimensional vector field is the extent to which the vector field flow behaves like a source or a sink at a given point. It is a local measure of its "outgoingness"—the extent to which there is more exiting an infinitesimal region of space than entering it.

If there is a source, it means net flux is going to be positive. Then it means flux $\oint_V {{\bf F}\cdot d{\bf a}}$ shows us that there is a source there. But why do we have to divide flux by "volume"?

I am asking the intuition behind defining divergence as flux divided by "volume".

user50322
  • 297
  • 7
    Try this: http://math.stackexchange.com/questions/150872/what-is-the-meaning-of-evaluating-the-divergence-at-a-point – SteveO Dec 17 '15 at 21:35
  • Voting to close as duplicate of the above pending clear distinction. The answer, though, is that you divide by volume because you're looking for average flux, not net flux; otherwise, divergence would simply be 0 everywhere, since net flux goes to 0 as volume goes to 0. – Pockets Dec 17 '15 at 21:39

1 Answers1

3

Flux is defined in "absolute terms", which is what creates the problem here.

To illustrate this by example, think of $V$ as a screen and $\mathbf F$ as a constant vector field representing water flowing through the screen $V$ (at a constant rate everywhere). This example shows two problems if we don't divide by $|V|$ in our divergence equation, where our intuition about divergence is that it measures to what extent $\mathbf F$ is a source/sink.

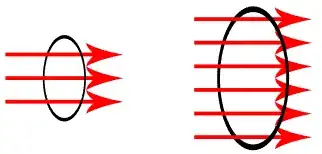
enter image description here

In our example, taking $V$ to be large makes $\oint_V \mathbf F \cdot d\mathbf a$ large, and taking $V$ small makes $\oint_V \mathbf F \cdot d\mathbf a$ small. So this is not by itself a good measure of the extent to which $\mathbf F$ is a source/sink, since we know that $\mathbf F$ is constant. Hence $\oint_V \mathbf F \cdot d\mathbf a$ is only really a measure of whether $\mathbf F$ is a source/sink.

Moreover, if $\mathbf F$ is not constant, it could be letting water flow into or out of the screen at different rates in different places, and hence $\oint_V \mathbf F \cdot d\mathbf a$ only measures whether $\mathbf F$ is a net source/sink over the region $V$. To test whether $\mathbf F$ is a source/sink at a point $\mathbf p$, we would approximate by taking a region $V$ about $\mathbf p$ and computing $\oint_V \mathbf F \cdot d\mathbf a$. Again, as $V$ shrinks down to $\mathbf p$, it has $0$ volume, so the integral goes to $0$, and we don't get a very useful measure. So we should instead consider the value of the integral relative to the size of $V$ as we shrink $|V|$ to $0$, thus getting a limit as is familiar with derivatives.

Jon Warneke
  • 4,937