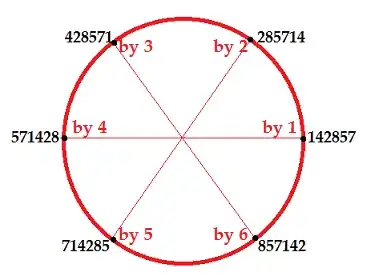
It is easy to verify that $$\frac 17=\frac {142857}{999999}$$ where $142857$ is the decimal period of $\frac 17$.
This period, which has six different digits, has the property that when multiplied by $1,2,3,4,5,6$, the respective products have the same six different digits in different position (Clearly, multiplied by $7$ must give $999999$).
Is $ 142857 $ the only six-digit number that has this property?