3

Given $g(x)=\frac{x}{2}+\frac{1}{x}$, is it possible to find an expression for $g^k(x)=(g\underbrace{\circ \cdots \circ}_k g)(x)$, where $k$ is some positive whole number?

For example, given $h(x)=\frac{x}{2}$, the expression for $h^k(x)$ is $h^k(x)=\frac{x}{2^k}$.

user299248
  • 33
  • Trivially, $g^k(\pm\sqrt{2}) = \pm\sqrt{2}$, but I'm not sure what else to say about the function. I wish I knew more! – feralin Dec 16 '15 at 21:34
  • The only rational functions whose iterates I know a reasonable way of writing down are the fractional linear transformations $\frac{ax + b}{cx + d}$. Beyond that case I think things get quite complicated; see, for example, https://en.wikipedia.org/wiki/Complex_dynamics. – Qiaochu Yuan Dec 16 '15 at 21:40

1 Answers1

1

Looking at $$ g(x)=\frac{x}{2}+\frac{1}{x} = \frac{x^2 + 2}{2x} $$

and cranking some iterations through the Maxima CAS, I get $$ g^2(x) = {{x^4+12\,x^2+4}\over{4\,x^3+8\,x}} \\ g^3(x) = {{x^8+56\,x^6+280\,x^4+224\,x^2+16}\over{8\,x^7+112\,x^5+224\,x^3+ 64\,x}} \\ g^4(x) = {{x^{16}+240\,x^{14}+7280\,x^{12}+64064\,x^{10}+205920\,x^8+256256 \,x^6+116480\,x^4+15360\,x^2+256}\over{16\,x^{15}+1120\,x^{13}+17472 \,x^{11}+91520\,x^9+183040\,x^7+139776\,x^5+35840\,x^3+2048\,x}} $$ This gives no simple pattern I am able to spot, just more or less complicated rational functions with nominator degree $2^k$ and denominator degree $2^k - 1$, and the proper coefficients to go asymptotically to $h^k$.

Here are plots of $\text{id}, g, g^2, g^3, g^4, g^5$:

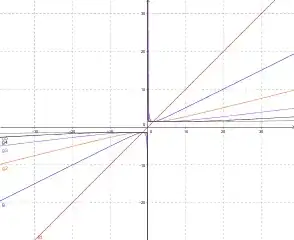enter image description here (Larger version)

This is slightly more interesting, as we see that for $x > 0$ the series $g^k$ seems to iterate against a constant function, at value of the positive fixed point $x_+^*$ of $g$. (Similar for the negative arguments against $x_-^*$).

Going for the fixed points: $$ x = g(x) = \frac{x^2 + 2}{2x} \Rightarrow \\ 2 x^2 = x^2 + 2 \Rightarrow \\ x^2 = 2 \Rightarrow \\ x = \pm \sqrt{2} $$

mvw
  • 34,562
  • I guess it's not really easy, maybe impossible, to find $g^k(x)$ because the formulas for $g^2,g^3,g^4...$ grow longer to write down... – user299248 Dec 16 '15 at 21:48
  • $g^4(x)$ is simpler than $${{x^{16}+240,x^{14}+7280,x^{12}+64064,x^{10}+205920,x^8+256256 ,x^6+116480,x^4+15360,x^2+256}\over{16,x^{15}+1120,x^{13}+17472 ,x^{11}+91520,x^9+183040,x^7+139776,x^5+35840,x^3+2048,x}}$$. Coming up with a formula or recurrence for the coefficients might be possible, but do I want it? – mvw Dec 16 '15 at 21:52