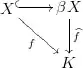Which spaces can be used as "test spaces" for the Stone-Čech compactification?

Question

Stone-Čech compactification $\beta X$ of a completely regular space $X$ is defined by the following property: Let $X$ be a completely regular space. Let $i \colon X \hookrightarrow \beta X$ be an embedding into a compact Hausdorff space $\beta X$. Then for every continuous map $f\colon X \to K$ where $K$ is a compact Hausdorff space there exists a unique continuous map $\widehat f \colon \beta X \to K$ such that $\widehat f \circ i =f$. (In the other words, every continuous map $X\to K$ has a continuous extension $\beta X\to K$.)

http://presheaf.com/?d=d4l86n4i40s4n18675m3rw6cye1p

It is known that if we require the above property to be true not for all compact Hausdorff spaces $K$ but only for $K=[0,1]$, i.e. for the unit interval, then we get an equivalent definition. (One possible argument to show this is based on the fact that every compact Hausdorff space embeds into a power of the unit interval.)

My question is:

Which (compact Hausdorff) spaces $K$ has similar property as unit interval, i.e., the property that if we require the universal property from the definition of Stone-Čech compactification to hold only for this space $K$, then we obtain an equivalent definition? Is complete characterization known?

Are these spaces precisely the generators of the reflective subcategory $\mathbf{CHaus}$ of the category $\mathbf{Top}$? Here $\mathbf{CHaus}$ denotes the category of compact Hausdorff spaces, $\mathbf{Top}$ is the category of topological spaces. By a generator of a reflective subcategory I mean a space such that its reflective hull is precisely this subcategory.

For example, this is true if we take the unit circle $S$, simply because $[0,1]$ is a closed subspace of $S$.

If we take $K=\{0,1\}$ with the discrete topology, then we cannot repeat the same argument as for unit interval. (Not every compact space, is a subspace of some power $\{0,1\}^a$.) So the above is probably not true for $K=\{0.1\}$

Answer 1

Such "test spaces" are exactly the compact Hausdorff spaces that contain a subspace homeomorphic to $[0,1]$. Clearly any such space is a test space; conversely, suppose $[0,1]$ does not embed in $K$. Then in fact every map $[0,1]\to K$ is constant, since any path-connected Hausdorff space is arc-connected. So taking $X$ to be any path-connected completely regular space, every map $X\to K$ is constant. It follows that any compactification of $X$ satisfies your universal property for $K$. Thus $K$ is not a test space.

As for your second question, yes, these are the generators of CHaus as a reflective subcategory. For any test space $K$ and any compact Hausdorff space $X$, there is an embedding $i:X\to K^S$ for some set $S$ (this follows from the fact that $[0,1]$ embeds in $K$). Moreover, this embedding can be realized as the equalizer of a pair of maps $K^S\rightrightarrows K^T$ for some $T$: it is the equalizer of its cokernel pair $K^S\rightrightarrows Y$, and $Y$ is again compact Hausdorff, so $Y$ embeds in $K^T$ for some $T$. Composing the cokernel pair with the inclusion $Y\to K^T$, we get a pair of maps $K^S\rightrightarrows K^T$ whose equalizer is $i$. Thus $X$ is generated by $K$ using limits. Conversely, if $K$ is not a test space, then it is totally path-disconnected, and then it is easy to see that the reflective subcategory generated by $K$ consists entirely of totally path-disconnected spaces.