4

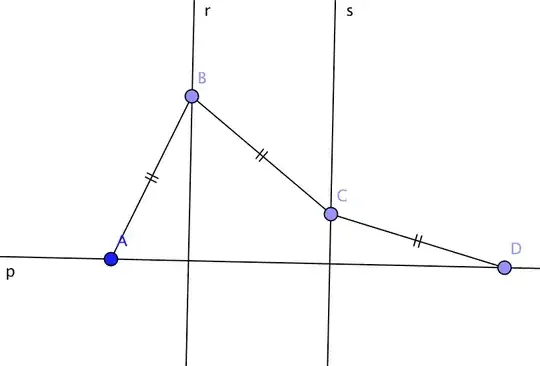
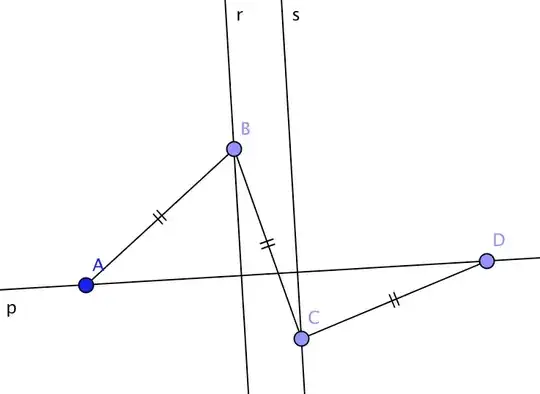
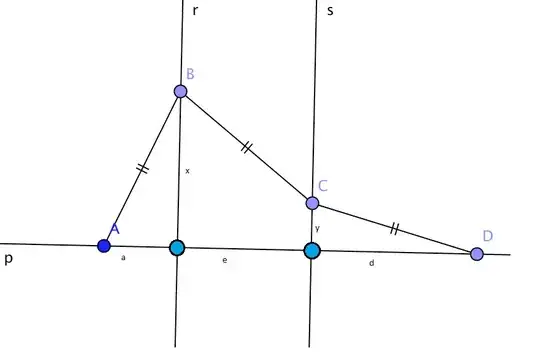
Given two parallel lines $r$ and $s$, line $p$, perpendicular to both, and points $A$ and $D$ on different sides of $p$ with respect to the parallel lines, how can I prove the existence of two points, $B$ and $C$, respectively on $r$ and $s$, such that segments $AB$, $BC$ and $CD$ are congruent?

I'd prefer a constructive proof, for it to be a more general solution useful to solve this question too. (also, geometric proofs are fun)

Here are two examples I constructed in reverse (I fitted the lines to the points and not viceversa): example 1 example 2

Community
  • 1
sebgiles
  • 313

1 Answers1

3

Let $a,x,d,y$ the distances shown in the picture and $t=\overline{AB}=\overline{BC}=\overline{CD}$

enter image description here

Then we have

$$a^2+x^2=t^2\tag{1}$$ $$d^2+y^2=t^2\tag{2}$$ $$(x-y)^2+e^2=t^2\tag{3}$$ If we add $a^2d^2$ to $(3)$ and reorder the terms we get $$x^2+a^2-2xy+y^2+b^2+e^2=t^2+a^2+d^2$$ an further $$2xy=t^2+e^2-a^2-d^2\tag{4}$$ if we substitute by $(1)$ and $(2)$. Squaring $(5)$ and substituting again by $(1)$ and $(2)$ gives $$4(t^2-a^2)(t^2-d^2)=(t^2+e^2-a^2-d^2)^2\tag{5}$$ $(5)$ is an equation of degree $4$ in $t$ but quadratic in $t^2$: $$3t^4-2t^2(a^2+d^2+e^2)+(2a^2d^2+2a^2e^2+2d^2e^2)-(a^4+d^4+e^4)=0$$ So it can be easily solved. The discriminant $\Delta$ of the quadratic equation satisfies $$\frac{1}{8}\Delta=(a^2-d^2)^2+(a^2-e^2)^2+(d^2-e^2)^2\ge0$$ For the second picture we could start with the equations

$$a^2+x^2=t^2$$ $$d^2+y^2=t^2$$ $$(x+y)^2+e^2=t^2\tag{6}$$

but we would get the same solutions because the equations differ only in the sign of $y$ in $(6)$

miracle173
  • 11,049
  • Hmm, this is great, since I had no proof at all before I asked the question. However I was hoping for a geometric proof. Should I ask a new question or is it fair that I edit this one? – sebgiles Dec 16 '15 at 08:21
  • for me it is ok if you edit your question in such a way that it does not invalidate my answer, e.g. you can add, that you prefer a geometric proof. – miracle173 Dec 16 '15 at 08:34
  • Are these solutions for $t^2$ real and positive? – Empy2 Dec 16 '15 at 09:07
  • @Michael At least one solution for $t^2$ is a positive real. It is also possible to have two positive values for $t^2$. As far as construction is concerned, it can easily be proven that $t$ is constructible with a straightedge and a compass. However, the construction seems very tedious. – Batominovski Dec 16 '15 at 09:22
  • @Michael: I didn't check this. But the OP shows that there are triples $(a,d,e)$ where at least one solution exists. – miracle173 Dec 16 '15 at 09:53