Let's consider the right triangle ABC with angle $\angle ACB = \frac{\pi}{2}$, $\angle{BAC}=\alpha$, D is a point on AB such that |AC|=|AD|=1; the point E is chosen on BC such that $\angle CDE=\alpha$. The perpendicular to BC at E meets AB at F. I'm supposed to calculate:
$$\lim_{\alpha\rightarrow0} |EF|$$
Below is the construction described in the question:
$\hspace{3.5cm}$
The Inscribed Angle Theorem says that $\angle DCB=\angle DCE=\alpha/2$. Since $\angle CDE=\alpha$ by construction, the exterior angle $\angle DEB=3\alpha/2$.
Since $\angle DBE=\pi/2-\alpha$, as $\alpha\to0$, $\triangle DBE$ and $\triangle DBC$ get closer to right triangles with $$ \frac{|BE|}{|DB|}\tan(3\alpha/2)\to1\quad\text{and}\quad\frac{|BC|}{|DB|}\tan(\alpha/2)\to1 $$ Thus, $$ \frac{|BE|}{|BC|}\frac{\tan(3\alpha/2)}{\tan(\alpha/2)}\to1 $$ Therefore, by similar triangles and because $\lim\limits_{x\to0}\frac{\tan(x)}{x}=1$, $$ \frac{|FE|}{|AC|}=\frac{|BE|}{|BC|}\to\frac13 $$ Since $|AC|=1$, we have $$ \lim_{\alpha\to0}|FE|=\frac13 $$
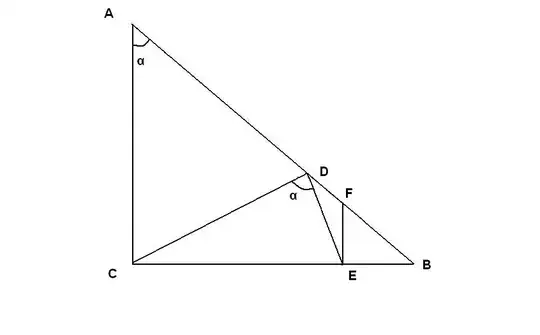
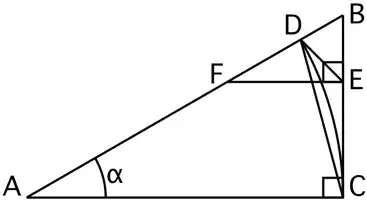
We do a computation similar to the one by robjohn. Let $\alpha=2\theta$. By angle-chasing, we can express all the angles in the picture in terms of $\theta$.
Since $\triangle ACD$ is isosceles, $CD=2\sin\theta$. Now we compute $DE$ by using the Sine Law. Note that $\angle CED=\pi-3\theta$ and $\angle DCE=\theta$. Thus $$\frac{DE}{\sin\theta}=\frac{CD}{\sin(\pi-3\theta)}=\frac{CD}{\sin 3\theta},$$ and therefore $$DE=\frac{2\sin^2\theta}{\sin 3\theta}.$$ Now use the Sine Law on $\triangle DEF$. We get $$\frac{EF}{\sin(\pi/2+\theta)}=\frac{DE}{\sin 2\theta}.$$ Since $\sin(\pi/2+\theta)=\cos\theta$, we get $$EF=\frac{2\sin^2\theta\cos\theta}{\sin 2\theta\sin 3\theta}.$$ Using the identity $\sin 3\theta=3\sin\theta-4\sin^3\theta$, we find the very simple result $$EF=\frac{1}{3-4\sin^2\theta},$$ and therefore the limit is $1/3$.
