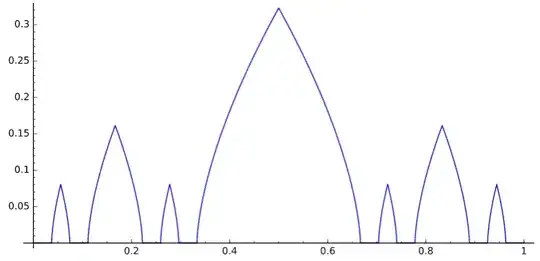
I have recently been introduced to the concept of Holder condition and I was told that there are functions that are Holder continuous but whose variation in unbounded.
Can anyone present an example, with explanation of both unboundedness of variation and Holder condition? If possible some example that's not too complicated and doesn't require advanced math - Let's say, I looked up the Weierstrass function and that's quite out of my reach at the moment.
Let $C\subset [0,1]$ be the standard Cantor set. Define $$f(x)=(\operatorname{dist}(x,C))^{\alpha}$$ with $\alpha\in (0,1)$ to be chosen later. This is an $\alpha$-Hölder continuous function since it's a composition of the Lipschitz function $x\mapsto \operatorname{dist}(x,C)$ with the $\alpha$-Hölder function $t\mapsto t^\alpha$.
The complement of Cantor set has $2^{k-1}$ intervals of length $3^{-k}$, for each $k=1,2,\dots$. On such an interval, $f$ increases from $0$ to $(3^{-k}/2)^\alpha$ and then decreases to $0$. Therefore, its total variation is
$$
\sum_{k=1}^\infty 2^{k-1} (3^{-k}/2)^\alpha
$$
and this series diverges when $\alpha\le \log 2/\log 3$.
This is a fairly simple function that you can sketch by hand. The case $\alpha = \log 2/\log 3$ is particularly nice: each new generation of peaks is half the height of the previous ones, so that the sum of heights is the same in each generation.
