I am not expecting to get an exact answer but some arguments will be appreciated. Thanks.
-
5Have you looked at this question: http://math.stackexchange.com/questions/455626/what-does-limit-actually-mean?rq=1 What is it in that answer that's not clear to you or in what way is that answer not satisfactory? It's not clear what your question actually is. – skyking Dec 02 '15 at 13:06
5 Answers
$f(x)$ is a function, and we put numbers into this function and it gives us numbers back. If $f(x)$ tends to a limit as $x$ tends to infinity, then it means that if we a really big number into the function, it will behave in a certain way. So what happens if we put progressively bigger and bigger numbers into the function? This is what the limit is.
For example, let's look at $f(x) = 0$. This is a constant function, and no matter what $x$ we choose, it spits out $0$. If we put in a really big $x$ then, it doesn't matter, we still get $0$ back. As $x$ goes to infinity, it still doesn't affect the output, the function still returns $0$. Thus, the limit of the function as $x$ goes to infinity is simply $0$.
Now lets consider $f(x)= 1/x$. If we put in say $1000$, then we find that $f(1000) = 1/1000$. This is pretty small, but if we choose an even bigger $x$, then we can make it even smaller. For example $f(10000) = 1/10000$. It turns out that the bigger the number we choose, the closer to $0$ this function gets. What this tells us is that as the number we put in to the function, $x$, approaches infinity (getting bigger and bigger), the function spits out numbers that get closer and closer to $0$. Thus, the limit of the function is $0$.
- 398
Imagine you have a cake with a volume $C$ and $f(x)$ is the volume of your cake slice if it is sliced into $x$ slices. So $f(x) = \frac{C}{x} $.
What will the happen to the volume of your cake slice as the number of slices increases? It will get smaller and smaller and if $x$ could possibly reach infinity, $f(x)$ would be 0.
In other words even though $x$ tends to infinity, $f(x)$ tends to $0$. Or though $x$ tends to infinity $f(x)$ tends to a limit. Or in symbolic terms:
$$\lim_{x\rightarrow \infty}f(x)=0=L.$$
- 405
-
I am looking more into how we define it . If I imagine that a limit is zero. We can easily check that . But if I say the limit tends to infinity, how Can you say that it doesn't stop at a particular number but goes to infinity . If this doesn't make sense then I will comment again. Thanks – Abu Bardewa Dec 02 '15 at 13:10
-
@Abu But it will not "stop at a particular number" it will increase forever more. That's why we need the $\lim$ notation as infinity is not well defined. – BLAZE Dec 02 '15 at 13:19
-
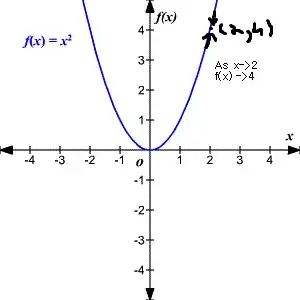
Okay, I think I understand your question. If the values you are substituting (x) increase up to infinity, the answer you get when you substitute (f(x)) may do one of three things: either it too increases to infinity or it decreases to negative infinity or it tends towards a limit L, like in the cake example. Its easy to imagine a limit that tends to infinity as well. What will happen to the area of a square, with side length x, if I increase x to infinity? f(x)=x^2. Does this answer it or do you want a formal definition? – Pieter Rousseau Dec 02 '15 at 13:20
-
I think U understand what I am asking. . This problem arose while doing a graph sketching of a rational functions . So I started thinking about the limits . Yes, I would like a formal definition please . Thanks – Abu Bardewa Dec 02 '15 at 13:24
-
Yes, graphs are most helpful to visualise the limits at infinity, because the horizontal asymptote is this L that the function is tending to as x is tending to infinity. – Pieter Rousseau Dec 02 '15 at 13:35
-
Formal definition: if lim_{x->oo} f(x) = L then for all e>0 there exists a c so that abs(f(x)-L)<e. So basically it means if you give me any number e>0, then I can find a number c from the domain so that if I substitute any number bigger than c, then the difference between f(x) I get and the limit L will be smaller than your number e. So no matter how small you make e (except 0), I can find a number to substitute into f(x) to get near enough to L so that abs(f(x)-L) is less than your number e. – Pieter Rousseau Dec 02 '15 at 13:38
Say there's a function $f(x) = x^2$ Now, say that you bring $x$ closer and closer to $2$ When $x = 1.9, f(x) = 3.61$ When $x = 1.999, f(x) = 3.996001$
So as $x\to 2, \ f(x) \to 4$ which can also alternatively be expressed as: $\lim_{x\to2} f(x) = 4$
Similarly, say there's a function $f(x) = 1/x$. as $x$ gets larger, the value of $f(x)$ gets smaller. The larger we make the value of $x$, the smaller the value of $f(x)$ we obtain. Now we can make $x$ as large as we like. The closer it gets to infinity, the closer $f(x)$ gets to $0$ Therefore as $x \to \infty, f(x) \to 0$ or in other notation, $lim_{x\to \infty} f(x) = 0$
- 168
$\fbox{$\text{A limit is the value that a function "approaches" as the index approaches some value}$.}$
If the function approaches infinity in the limit, then the index will increase forever more until a value is reached, if a finite value is not reached we say the limit diverges.
Here is a graphical derivative definition involving limits, it may hone your intuition a little but it is not a direct answer to your question.
Here is the precise $(\varepsilon, \delta)$ definition of the limit of a function; Let $f : D \rightarrow \mathbb{R}$ be a function defined on a subset $D \subseteq \mathbb{R}$ , let $c$ be a limit point of $D$, and let $L$ be a real number. Then the function $f$ has a limit $L$ at $c$ is defined to mean for all $\varepsilon \gt 0$, there exists a $\delta \gt 0$ such that for all $x$ in $D$ that satisfy $0 \lt | x - c | \lt \delta$ , the inequality $|f(x) - L| \lt \varepsilon$ holds.
Symbolically:
$$\lim_{x \to c} f(x) = L \iff (\forall \varepsilon \gt 0)(\exists \ \delta > 0) (\forall x \in D)(0 < |x - c | < \delta \ \Rightarrow \ |f(x) - L| < \varepsilon)$$
However, it can sometimes be better to answer this question with a typical example;
If $$f(x)=\frac{4x^2 + 6x + 2}{x^2 + 2x + 1}$$ To handle limits involving fractions you factor out the dominant term from top and bottom such that they cancel, by dominant term; I mean the term of highest degree, in this case it's $x^2$: $$\lim_{x\to\infty} \frac{4x^2 + 6x + 2}{x^2 + 2x + 1}$$ $$=\require\cancel\lim_{x\to\infty} \frac{2\cancel{x^2}\left(2 + \frac{3}{x} + \frac{1}{x^2}\right)}{\cancel{x^2}\left(1 + \frac{2}{x} + \frac{1}{x^2}\right)}$$ $$=\lim_{x\to\infty} \frac{2\left(2 + \frac{3}{x} + \frac{1}{x^2}\right)}{1 + \frac{2}{x} + \frac{1}{x^2}}\tag{1}$$ $$=\frac{2\left(2 + 0 + 0\right)}{1 + 0 + 0}\tag{2}$$ $$={4}$$
You get from $(1)$ to $(2)$ by making the observation that each of the fractions with $x$ or $x^2$ in the denominator will equal zero in the limit as $x$ tends to infinity.
This is what it means for a function $f(x)$ to approach a value or limit if you prefer (in this case $4$) as $x$ tends to infinity.
With knowledge of basic first-order logic, it is possible to define the meaning of this phrase with brutal precision. If you don't know any first-order logic, I suggest making good use of the internet to learn more about it, since it is basically the most fundamental system of ideas in all mathematics.
Anyway, lets go ahead and be precise.
Define a function $P : \mathbb{R}^\mathbb{R} \times \mathbb{R} \rightarrow \{\mathrm{true},\mathrm{false}\}$ as follows:
$$P(f,y) \iff \mathop{\forall}_{\varepsilon \in \{\mathbb{R} > 0\}} \mathop{\exists}_{\delta\in \{\mathbb{R} > 0\}} \mathop{\forall}_{x \in \{\mathbb{R}>\delta\}}|f(x)-y|<\varepsilon $$
Then the phrase "$f(x)$ tends to $y$ as $x$ tends to infinity" is a way of saying that $P(f,y)$ holds.
Now define $Q : \mathbb{R}^\mathbb{R}\rightarrow \{\mathrm{true},\mathrm{false}\}$ as follows:
$$Q(f) = \mathop{\exists}_{y\in \mathbb{R}} R(f,y)$$
Then the phrase "$f(x)$ tends to a limit as $x$ tends to infinity" is a way of saying that $Q(f)$ holds.
- 67,744