0

I need to find the equation for the line tangent to the curve:

$$ x = 2\cos t, y = 2\sin t, t = \frac \pi4 $$

I also need to find the value of: $$ \frac{d^2y}{dx^2} $$

I'm not too sure what to do.. I got the slope of -1 by doing $\frac{dy}{dx}$ which let to $-cott$ and plugging in $\frac \pi4$

Any help on getting the rest of the problem done would be greatly appreciated.

janmarqz
  • 10,538
bankey
  • 331
  • Would I make a unit circle where $x^2 + y^2 = 1$ ? But what happens to the 2 before the $sin$ and $cos$? Would it be $x^2 + y^2 = 1/2$ ? This is me thinking out loud – bankey Dec 01 '15 at 02:39
  • check the similar http://math.stackexchange.com/questions/1072869/why-doesnt-it-work-when-i-calculate-the-second-order-derivative/1072948#1072948 and up-voted if it helps you ; ) – janmarqz Dec 01 '15 at 02:41
  • Afraid it doesn't – bankey Dec 01 '15 at 02:46
  • a formula there, would do the task, it is $\frac{d^2y}{dx^2}=\frac{\frac{d^2y}{dt^2}\frac{dx}{dt}-\frac{d^2x}{dt^2}\frac{dy}{dt}}{\left(\frac{dx}{dt}\right)^3}$ – janmarqz Dec 01 '15 at 02:51
  • @bankey You are correct that it makes a circle, but the radius is actually 2. You can see this by setting $t=0$. – Ben Longo Dec 01 '15 at 03:24

1 Answers1

1

Disclaimer: My high school's Calculus I course does not teach parametric functions, and I haven't taken the course for even a full semester yet.

Finding the tangent line at $\frac {\pi}{4}$

One definition for cosine and sine is the coordinates of the unit-circle. A unit-circle is by definition said to be centered around the origin and to have a radius length of 1 unit. A slightly manipulated version of the standard formula for circles around the origin ($\sqrt{x^2+y^2}=r$) gives us: $$\sqrt{x^2 + y^2} = 1$$ If x and y ($\cos(x)$ and $\sin(x)$ respectively) are multiplied by 2 then: $$\sqrt{(2x)^2 + (2y)^2}$$ $$\sqrt{4x^2 + 4y^2}$$ $$\sqrt{4( x^2 + y^2 )}$$ $$2\sqrt{x^2+y^2}$$ Substituting $\sqrt{x^2+y^2}$ with r based upon the above equation gives us: $$2r$$ Which means that our new radius is 2 units long. The equation for a circle with a radius size of 2 units that is centered around the origin is: $$x^2 + y^2 = 4$$ Now we can take the derivative with respect to x: $$2x + 2y*y'(x) = 0$$ Solving for $y'(x)$ gives: $$y'(x) = -\frac xy$$ At a $45°$ angle, $\cos(x) = \sin(x)$, thus, $x = y$. Therefore $y'(\frac {\pi}{4}) = -1$. To find the tangent line, you now just need the y-intercept. This can be found by using the equation $y=mx+b$ like so: $$\sqrt{2}=-\sqrt{2} + b$$ $$b = 2\sqrt{2}$$ Now we put it all together, again using $y=mx+b$, to obtain the tangent line: $$y = -x + 2\sqrt{2}$$

For visual confirmation of the above tangent line, here's a graph from Wolfram Alpha:

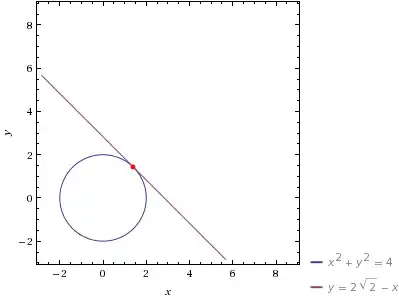
enter image description here

Finding a function for the second derivative:

By the quotient rule of derivatives, $y''(x)$ is: $$\frac {y-y'(x)*x}{y^2}$$ Subsitute $y'(x)$ with $-\frac {x}{y}$: $$y''(x) = \frac {y + \frac {x^2}{y}}{y^2}$$ Simplify: $$y''(x) = \frac {x^2 + y^2}{y^3}$$ We can optionally simplify further by using our circle equation $x^2 + y^2 = 4$: $$y''(x) = \frac {4}{y^3}$$ Finally, upon substitution of $2\sin(t)$ for y, we get: $$y''(x) = 2\csc(x)^3$$

CaptainObvious
  • 390