In the limit of $N \rightarrow \infty$, find solution $z$ to $\text{e}^{-(z+N)} \sum \limits_{k=0}^{N} \frac{(z+N)^k}{k!}=\frac{1}{2}$

Question

Fix an integer $N$, and consider the unique positive solution $z$ to the following equation:

$$\text{e}^{-(z+N)} \sum \limits_{k=0}^{N} \frac{(z+N)^k}{k!}=\frac{1}{2}$$

For $N = 0$, we find that $z = \ln(2) \approx 0.6931$. For $N=10$, the solution is $z \approx 0.6685$. It appears that as $N$ approaches infinity, $z$ is approaching a constant value (maybe $2/3$?). What constant is this approaching?

Motivation

This is an equation I derived to find the median (or rather, the difference between the mean and median) of a generalized exponential distribution. The case $N=0$ corresponds to the usual exponential distribution, or finding the inter-arrival times $\Delta t = t_1 - t_0$. Higher values of $N$ represent the elapsed time $t_{N+1} - t_0$.

Answer 1

If we let

$$ p_n(z) = \sum_{k=1}^{n} \frac{z^k}{k!}, $$

then the limit linked by Lucian in the comments can be written as

$$ \frac{p_n(n)}{\exp(n)} = \frac{1}{2} + o(1) \qquad \text{as } n \to \infty, \tag{1} $$

and as Aryabhata notes this can be found in Donald J. Newman's book A Problem Seminar. This limit is a special case of the following, due to Donald J. Newman and Theodore J. Rivlin${}^1$:

$$\DeclareMathOperator{erfc}{erfc} \frac{p_n(n+w\sqrt{n})}{\exp(n+w\sqrt{n})} = \frac{1}{2}\erfc\!\left(\frac{w}{\sqrt{2}}\right) + o(1) \qquad \text{as } n \to \infty, \tag{2} $$

where $\erfc$ is the complementary error function and the error term $o(1)$ is uniform with respect to $w$ for $w$ in compact subsets of $\mathbb C$. Indeed, since $\erfc(0) = 1$, limit $(1)$ follows from limit $(2)$ by setting $w=0$.

Now, the expression in your question is obtained by setting $w = z/\sqrt{n}$, but the asymptotic

$$ \begin{align} \frac{p_n(z+n)}{\exp(z+n)} &= \frac{1}{2}\erfc\!\left(\frac{z}{\sqrt{2n}}\right) + o(1) \\ &= \frac{1}{2} - \frac{z}{\sqrt{2\pi n}} + O(n^{-1}) + o(1) \qquad \text{as } n \to \infty, \tag{3} \end{align} $$

where in the second line we've used the Maclaurin series for $\erfc$, doesn't given us enough information to determine the $o(\sqrt{n})$ roots of your equation

$$ \frac{p_n(z+n)}{\exp(z+n)} = \frac{1}{2}. $$

Indeed, after substituting this into $(3)$ we see that to first order they must satisfy

$$ \frac{z}{\sqrt{2\pi n}} = o(1) \qquad \text{as } n \to \infty, $$

and we evidently need more information how this $o(1)$ error term balances with $1/\sqrt{n}$. In other words, we need more accurate information about the rate of convergence to the limit in $(2)$.

This information was obtained by Kriecherbauer et al.${}^2$ using a version of the Riemann-Hilbert method. After some massaging their Theorem 3.3 gives us the asymptotic

$$ \frac{p_n(n\zeta)}{\exp(n\zeta)} = \frac{1}{2}\erfc\!\left(\sqrt{n\varphi(\zeta)}\right) + \frac{(n\zeta e^{-\zeta})^n}{n!} - \frac{\exp(-n\varphi(\zeta))}{3\sqrt{2\pi n}} + o(n^{-1/2}), \tag{4} $$

where

$$ \varphi(\zeta) = \zeta - 1 - \log\zeta $$

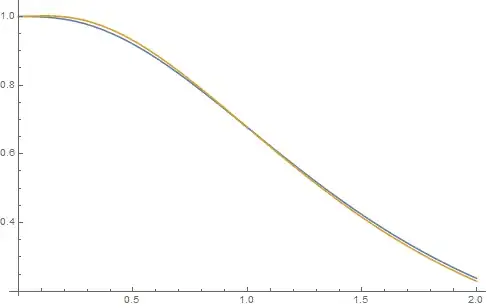
and the correct branch of $\sqrt{}$ must be chosen, which is valid in the limit $n \to \infty, \zeta \to 1$. One can check that this is a very good approximation even for small values of $n$. Here's a plot of the left-hand side of $(4)$ in blue versus the right-hand side in orange for $0 < \zeta < 2$ and $n=2$:

Substituting $\zeta = 1+z/n$ then expanding everything in series and collecting like terms yields

$$ \frac{p_n(z+n)}{\exp(z+n)} = \frac{1}{2} + \frac{2-3z}{3\sqrt{2\pi n}} + o(n^{-1/2}) \qquad \text{as } n \to \infty, \tag{5} $$

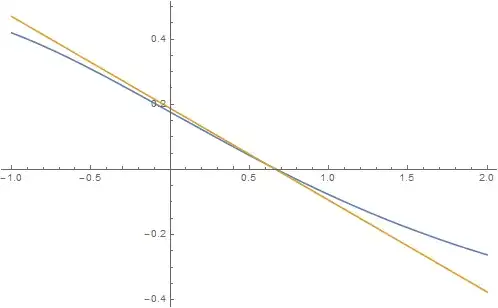
where the error holds uniformly for $z = o(\sqrt{n})$. Below is a plot of $e^{-z-n} p_n(z+n) - 1/2$ in blue versus $(2-3z)/3\sqrt{2\pi n}$ in orange for $0 < z < 1$ and $n=2$:

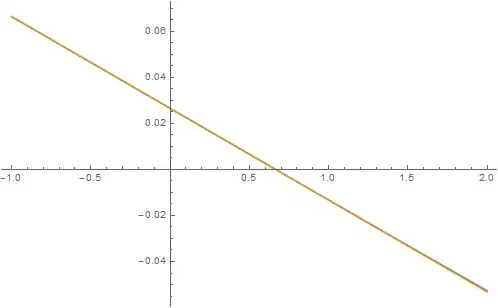
and for $n=100$:

It then follows that the $o(\sqrt{n})$ roots of the equation

$$ \frac{p_n(z+n)}{\exp(z+n)} = \frac{1}{2} $$

must satisfy

$$ 0 = \frac{2-3z}{3\sqrt{2\pi n}} + o(n^{-1/2}) \qquad \text{as } n \to \infty, $$

and solving for $z$ yields

$$ z = \frac{2}{3} + o(1) \qquad \text{as } n \to \infty. $$

It's worth noting that your equation has many complex roots which are $\Theta(\sqrt{n})$ and are picked up by limit $(2)$ above, and many which are $\Theta(n)$ which require a different asymptotic to detect.

---

1. D. J. Newman and T. J. Rivlin
   The zeros of the partial sums of the exponential function
   J. Approx. Theory 5 (1972), 405–412.

2. T. Kriecherbauer, A. B. J. Kuijlaars, K. D. T.-R. McLaughlin, and P. D. Miller
   Locating the zeros of partial sums of $e^z$ with Riemann-Hilbert methods
   Integrable Systems and Random Matrices, Contemp. Math., vol. 458, Amer. Math. Soc., Providence, RI, 2008, pp. 183–195.
   arXiv link

Answer 2

Your equation can be re-written in the form $$ Q(N + 1,N + z) = \tfrac{1}{2}, $$ where $Q$ denotes the normalised incomplete gamma function. Consider the more general problem of finding the $z$-root of the equation $$ Q(N + 1,N + z) = q $$ for a given $0<q<1$ and positive integer $N$. It is shown in this paper that \begin{align*} z \sim 1 + \tau _0 (N + 1)^{1/2} + \frac{{\tau _0^2 - 1}}{3} &+ \frac{{\tau _0^3 - 7\tau _0 }}{{36(N + 1)^{1/2} }} \\ &- \frac{{3\tau _0^4 + 7\tau _0^2 - 16}}{{810(N + 1)}} + \frac{{9\tau _0^5 + 256\tau _0^3 - 433\tau _0 }}{{38880(N + 1)^{3/2} }} + \ldots \end{align*} as $N\to+\infty$ provided $\log (q(1 - q)) = o(N)$. Here $\tau_0$ is the unique real root of the equation $$ q = \tfrac{1}{2}\operatorname{erfc}(2^{ - 1/2} \tau _0 ), $$ with $\operatorname{erfc}$ being the complementary error function. The paper contains an algorithm to generate the coefficients of the asymptotic expansion. In the special case that $q=\frac{1}{2}$, $\tau_0$ is $0$ and therefore we have $$ z \sim \frac{2}{3} + \frac{8}{{405(N + 1)}} + \frac{{184}}{{25515(N + 1)^2 }} + \frac{{2248}}{{3444525(N + 1)^3 }} + \ldots $$ as $N\to+\infty$. This may be re-expanded in inverse powers of $N$ instead of $N+1$: $$ z \sim \frac{2}{3} + \frac{8}{{405N}} - \frac{{64}}{{5103N^2 }} + \frac{{2944}}{{492075N^3 }} + \ldots, $$ as $N\to+\infty$.