0

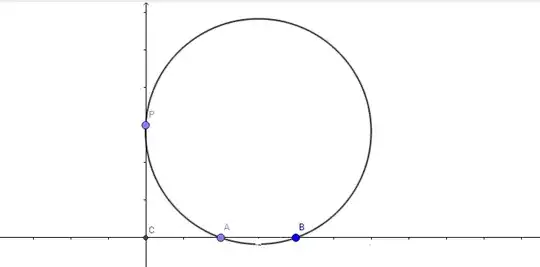
enter image description here

I have the following problem. In the figure, the circumference is tangent to the Y-axis in the point P, the point A has coordinates (2,0) and OA=AB. I am asked to calculate the coordinates of the point P.

This is what I thought: I want to calculate the center of the circumference, given that I know the coordinates of two points in it. If I call this center C, then, for example, AC=PC, and knowing what the distance between two points is, I'd be able to find the coordinates of the point P. However, I am not being able to find the coordinates of the center.

I am supposed to be able to solve this with a not so advanced math. Any ideas?

Encontro Regional Sul
  • 47
  • I don't see what's random here or exactly what you mean by $OA=OB$. – Math1000 Nov 27 '15 at 18:54
  • Oh, sorry. O is the origin of the plane (where there is what looks like a C). And I wanted to calculate the center knowing the coordinates of the points A and B. – Encontro Regional Sul Nov 27 '15 at 18:58
  • Three points define a circle; see here for various ways of finding the center and radius: http://math.stackexchange.com/questions/213658/get-the-equation-of-a-circle-when-given-3-points – Math1000 Nov 27 '15 at 19:13

1 Answers1

0

The center of the circle is $(3, b)$. $3$ came from mid point between A and B, and it's also the radius of the circle. And $$b^2=r^2-1^2=3^2-1=8$$ So $P=(0,2\sqrt2)$.

Kay K.
  • 9,931