5

While doing some caculation related to von Neumann entropy, I encountered this kind of convergent series. $$\text{Exl}(x) \equiv \sum _{n=1}^{\infty } \frac{x^n \log (n!)}{n!}$$ In my calculation, this function Exl$(x)$ appears in some places where exponential function should be, for example, $$\frac{\cosh (x) \text{Cxl}(x) + \sinh (x)\text{Sxl}(x)}{\cosh(2x)}$$ appears in my calculation, where $$\text{Cxl}(x) \equiv \frac{\text{Exl} (x) +\text{Exl} (-x)}{2}$$ and $$\text{Sxl}(x) \equiv \frac{\text{Exl} (x) -\text{Exl} (-x)}{2}$$ are defined from the similarity to the hyperbolic functions. 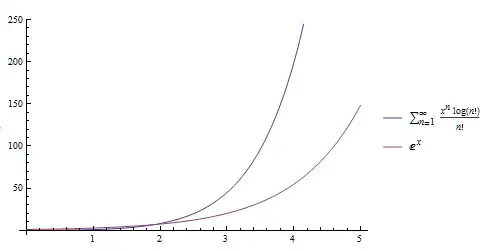As the given function Exl$(x)$ looks like some kind of 'augmented' exponential function as the following plot suggests, enter image description here

I suspect there's a well defined special function related to this series. Is it so? Any kind of suggestion is appreciated.

Michael Rozenberg
  • 194,933
generic properties
  • 1,100
  • For large $x$, $\operatorname{Exl}(x)$ is larger than $e^x$ by a factor of roughly $x\log(x)$. Specifically, $\operatorname{Exl}(x) \sim x \log(x) e^x$ as $x \to \infty$. – Antonio Vargas Nov 25 '15 at 20:57
  • @AntonioVargas : Thank you. But since I am not familiar with the asymptotic analysis, it is not clear to me how you obtained that asymptotic form. Can you give me some hint? – generic properties Nov 27 '15 at 03:39
  • Sure, I'll try to write an answer soon. – Antonio Vargas Nov 27 '15 at 08:37
  • @AntonioVargas : Well, my guess is that the major contribution to the sum is from the $n \approx x$ term, so we pick up that term and use the Stirling's approximation twice, once for the $\text{log}(x)$ and another for the $x^x$ in the denominator. But I'm not sure how I can justify this is rigorous. Am I right? – generic properties Nov 28 '15 at 16:45
  • I would agree with that :). After using Stirling's formula I compared the sum to an integral to derive the asymptotic. – Antonio Vargas Nov 28 '15 at 16:56
  • @Antonio Vargas : I'm sorry to bother, but can we predict its behavior as $x \to -\infty$ ? Equivalently, what is the behavior of $\text{Cxl}(x)$ as $x \to \infty$ ? My guess is $\text{Exl}(x) \to -x \log (x) e^{-x}$ but numerical calculation says otherwise... – generic properties Nov 30 '15 at 16:30

1 Answers1

4

I suspect there's a well defined special function related to this series. Is it so ?

Not really. Basically, $\text{Exl}(x)=-F'(1),$ where $F(k)=\displaystyle\sum_{n\ge0}\frac{x^n}{n!^k}~.~$ The only known values

of F are $F(0)=\dfrac1{1-x},~F(1)=e^x,$ and $F(2)=I_0\big(2\sqrt x\big).$ See Bessel function for more

information. Neither the function F, let alone its derivative, F', have ever been studied for

general values of the argument k. Alternately, we can use Stirling's approximation, but

neither $\displaystyle\sum_{n\ge1}\frac{x^n}{n!}\cdot\ln n$ nor $\displaystyle\sum_{n\ge0}\frac{x^n}{n!}\cdot n^k$ are expressible in terms of any known functions, be

they special or elementary. Well, that's not exactly true; the latter series yields the values

of Bell numbers for $x=1:$ see Dobinski's formula for more information.

Lucian
  • 48,334
  • 2
  • 83
  • 154