1

I have this limit problem:

$$\lim_{x\to\infty} \frac{x^2}{2x+1}\sin\frac{\pi}{x}$$

I had tried to solve it but I think I am using the wrong approach. Can anyone help me? My steps:

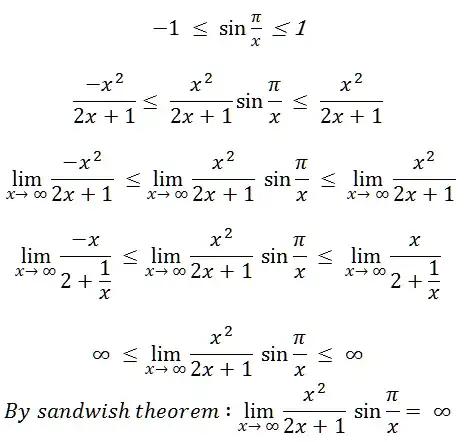
my attempt

user292965
  • 261

2 Answers2

5

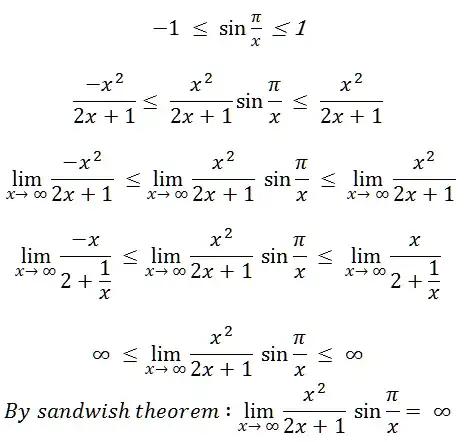
Hint: Our expression is equal to $$\frac{\pi x}{2x+1}\cdot\frac{\sin(\pi/x)}{(\pi/x)}.$$

André Nicolas
  • 507,029
  • Thank You! May I get more explanation, I cannot figure out how to get your equation. I am sorry.... – user292965 Nov 24 '15 at 05:10
  • I first brought one of the $x$ on top downstairs as $1/x$, getting $\frac{x}{2x+1}\frac{\sin(\pi/x)}{1/x}$. But I wanted a $\pi/x$ downstairs, which is easy, mutiply top and bottom by $\pi$. The motivation is that if we let $t=\pi/x$, we then have $\frac{\pi x}{2x+1}\frac{\sin t}{t}$. But it is standard that $\frac{\sin t}{t}\to 1$ as $t\to 0$. And the behaviour of $\frac{\pi x}{2x+1}$ for large $x$ is familiar. – André Nicolas Nov 24 '15 at 05:16
2

Recall that the sine function satisfies the inequalities for $\pi\ge z \ge 0$

$$z\cos z\le \sin z\le z$$

Then, letting $z=\pi/x$ reveals

$$\frac{\pi \cos (\pi/x)}{x}\le \sin (\pi/x)\le \pi/x$$

Then, we have

$$\frac{\pi x \cos (\pi/x)}{2x+1} \le \frac{x^2}{2x+1}\sin(\pi/x)\le \frac{\pi x}{2x+1}$$

By the squeeze theorem, we obtain

$$\lim_{x\to \infty}\frac{x^2}{2x+1}\sin(\pi/x)=\pi/2$$

Community
  • 1
Mark Viola
  • 179,405
  • Hi thanks for your reply. I think I totally forget about that sine function satisfies the inequalities for z>0, may I know why? I think I need to read up on the basics again. Thank You! – user292965 Nov 24 '15 at 04:56
  • Sorry I am confuse, may I also know why πcos(π/x)/x becomes πxcos(1/x)/2x+1. I understand that u multiply x^2/2x+1. but why did cos(π/x) becomes cos(1/x). Thank you! – user292965 Nov 24 '15 at 05:07
  • You're welcome. My pleasure. – Mark Viola Nov 24 '15 at 05:21
  • As for the inequalities for the sine function, we can appeal to geometric arguments. SEE THIS – Mark Viola Nov 24 '15 at 05:22
  • Dr. MV, so can I assume that this inequalities is always true and use your approach to solve the question, whenever I see similar question? Thank You! – user292965 Nov 24 '15 at 05:30
  • $\sin z\le z$ is true for $z\ge0$. $\sin z\ge z\cos z$ is true for at least $0\le z\le \pi$. – Mark Viola Nov 24 '15 at 13:47