Successive conditional expectations with respect to different sigma-algebras

Question

I am new to the notion of conditional expectation w.r.t a sigma algebra.

If X is a random variable on probability space ($\Omega, \mathbb{F},\mathbb{P}$), where $\Omega$= {1,2,3} with $X(\omega)=\omega$. Take the uniform measure. Suppose $\mathbb{f_1}$ is a sub sigma algebra generated by partition {1},{2,3}, and $\mathbb{f_2}$ is a partition generated by {2},{1,3}.

What are $\mathbb{E}(X|\mathbb{f_1})|\mathbb{f_2}$,and $\mathbb{E}(X|\mathbb{f_2})|\mathbb{f_1}$?

I know for $\mathbb{E}(X|\mathbb{f_1})$ is constant on A={1} with value $\frac{\mathbb{E}(X\mathbb{1}_A)}{\mathbb{P(A)}}$, which is $\frac{1\cdot\frac{1}{3}}{1/3}=1$

And on B={2,3}, it has value $\frac{\mathbb{E}(X\mathbb{1}_B)}{\mathbb{P(B)}}=\frac{2/3+3/3}{2/3}=\frac{5}{2}$.

So let Y=$\mathbb{E}(X|\mathbb{f_1})$, $\mathbb{E}(Y|\mathbb{f_2})$ should be constant on {2} and on {1,3}. What do I compute next?

I get really confused. Can someone help me?

Answer 1

You asked about what '$E[X|\mathscr F_2] | \mathscr F_1$' is. I asked my stochastic calculus professor the same once, and e didn't know.

Likely, it's not a well-defined mathematical object considering $|\mathscr F_1$ is merely a notation. You asking about that seems to be analogous to asking what is $A|B$ in $P(A|B)$.

---

Anyway, let's try to focus on understanding $E[E[X|\mathscr F_2] | \mathscr F_1]$

$$X = 1 \times 1_{\{1\}} + 2 \times 1_{\{2\}} + 3 \times 1_{\{3\}}$$

---

Define $\mathscr F_1 := \sigma(\{1\},\{2,3\}) \subseteq \mathscr F (= 2^{\Omega} ?)$

$Z:= E[X|\mathscr F_1]$ is any random variable s.t.

1. $Z$ is $\mathscr F_1$-measurable:

$$\sigma(Z) \subseteq \mathscr F_1$$

2. $\forall F_1 \in \mathscr F_1$

$$\int_{F_1} Z d \mathbb P = \int_{F_1} X d \mathbb P $$

---

If $F_1 = \emptyset$,

$$\int_{\emptyset} Z d \mathbb P = \int_{\emptyset} X d \mathbb P $$

$$\int_{\emptyset} E[X|\mathscr F_1] d \mathbb P = \int_{\emptyset} X d \mathbb P = 0$$

If $F_1 = \{1\}$, then we have:

$$\int_{\{1\}} Z d \mathbb P = \int_{\{1\}} X d \mathbb P $$

$$\int_{\{1\}} E[X|\mathscr F_1] d \mathbb P = \int_{\{1\}} X d \mathbb P $$

$$ = \int_{\Omega} X 1_{\{1\}} d \mathbb P $$

$$ = E[ X 1_{\{1\}}] $$

$$ = E[ (1 \times 1_{\{1\}} + 2 \times 1_{\{2\}} + 3 \times 1_{\{3\}}) 1_{\{1\}}]$$

$$ = E[ 1 \times 1_{\{1\}}]$$

$$ = E[ 1_{\{1\}}]$$

$$ = P({\{1\}}) = 1/3$$

If $F_1 = \{2,3\}$, then we have:

$$\int_{\{2,3\}} Z d \mathbb P = \int_{\{2,3\}} X d \mathbb P $$

$$\int_{\{2,3\}} E[X|\mathscr F_1] d \mathbb P = \int_{\{2,3\}} X d \mathbb P $$

$$ = \int_{\Omega} X 1_{\{2,3\}} d \mathbb P $$

$$ = E[ X 1_{\{2,3\}}] $$

$$ = E[ (1 \times 1_{\{1\}} + 2 \times 1_{\{2\}} + 3 \times 1_{\{3\}}) 1_{\{2,3\}}] $$

$$ = E[ 2 \times 1_{\{2\}} + 3 \times 1_{\{3\}}] $$

$$ = 2 E[ 1_{\{2\}}] + 3 E[1_{\{3\}}] $$

$$ = 2 P({\{2\}}) + 3 P({\{3\}}) $$

$$ = 2 (1/3) + 3 (1/3) $$

$$ = 5/3 $$

---

If we let $A=\{1\}$, we can observe that

$$Z:= E[X|\mathscr F_1] = E[X|A]1_A + E[X|A^C]1_{A^C}$$

$$= (\frac{1/3}{P(A)})1_A + (\frac{5/3}{P(A^C)})1_{A^C}$$

$$= (1)1_A + (5/2)1_{A^C}$$

---

///ly, we have:

$$E[X|\mathscr F_2] = E[X|D]1_D + E[X|D^C]1_{D^C}$$

where $D=\{2\}$ and $\mathscr F_2 = \sigma(D)$

---

The principle underlying the last two sections is that for a countable $\Omega$ and $\mathscr E$ generated by a partition $E_1, E_2, ..., E_n, ...$, we have

$E[X|\mathscr E] = E[X|E_1]1_{E_1} + ... + E[X|E_n]1_{E_n} + ...$

Note that $\forall \omega \in \Omega, \exists ! n \in \{1, 2, ...\}$ s.t. $\omega \in E_n$. Hence, if $\omega_0 \in E_k$

$$E[X|\mathscr E] (\omega_0) = E[X|E_1]1_{E_1}(\omega_0) + ... + E[X|E_k]1_{E_k}(\omega_0) + ... + E[X|E_n]1_{E_n}(\omega_0)$$

$$=E[X|E_1](0) + ... + E[X|E_k](1) + ... + E[X|E_n](0)$$

$$=E[X|E_k]$$

---

In general, if we have a random variable $X$ in $(\Omega, \mathscr F, \mathbb P)$ and $\mathscr H \subseteq \mathscr G \subseteq \mathscr F$

$$E[E[X|\mathscr G]|\mathscr H] = E[X|\mathscr H] = E[E[X|\mathscr H]|\mathscr G]$$

This is called the tower property (from Probability w/ Martingales):

---

---

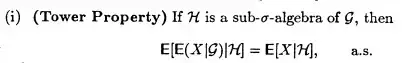
Here, we have

$$E[E[X|\mathscr F_2] | \mathscr F_1]$$

Now $\mathscr F_2 \subsetneq \mathscr F_1$ and $\mathscr F_1 \subsetneq \mathscr F_2$, but we can write:

$$E[E[X|\mathscr F_2] | \mathscr F_1] = $$

$$E[E[X|D]\ 1_D + E[X|D^C]1_{D^C} | \mathscr F_1]$$

$$E[E[X|D]\ 1_D| \mathscr F_1] + E[E[X|D^C]\ 1_{D^C}| \mathscr F_1]$$

$$E[X|D] \ E[1_D| \mathscr F_1] + E[X|D^C] \ E[1_{D^C}| \mathscr F_1]$$

where

$$E[1_D| \mathscr F_1] = E[1_D| A] 1_A + E[1_D| A^C] 1_{A^C}$$

and

$$E[1_{D^C}| \mathscr F_1] = E[1_{D^C}| A] 1_A + E[1_{D^C}| A^C] 1_{A^C}$$

Case is /// for $E[E[X|\mathscr F_1] | \mathscr F_2]$

---

Finally, if $E[X|\mathscr F_2] | \mathscr F_1$ would be a well-defined mathematical objects, it looks to be a random variable $W_0$ whose expectation is any random variable $W_1$ s.t.

1. $W_1$ is $\mathscr F_1$-measurable

2. $\forall F_1 \in \mathscr F_1$

$$\int_{F_1} W_1 d \mathbb P = \int_{F_1} E[X|\mathscr F_2] d \mathbb P$$

Now since

$E[X|\mathscr F_2]$ is any random variable $W_2$ s.t.

1. $W_2$ is $\mathscr F_2$-measurable

2. $\forall F_2 \in \mathscr F_2$

$$\int_{F_2} W_2 d \mathbb P = \int_{F_2} X d \mathbb P$$

I guess we have

$$\int_{F_1} W_1 d \mathbb P = \int_{F_1} W_2 d \mathbb P$$

$$\to \int_{F_1} E[W_0] d \mathbb P = \int_{F_1} W_2 d \mathbb P$$

Case is /// for $E[X|\mathscr F_1] | \mathscr F_2$