I read this example from Rudin's book but I can't understand what did he show by this example. Can anyone answer what does he mean by following?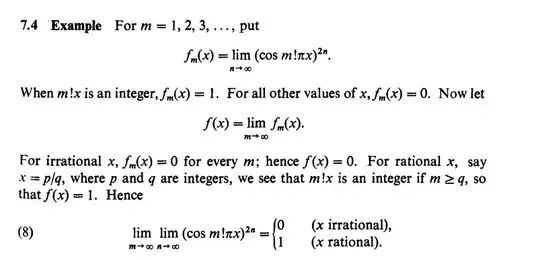
Asked
Active
Viewed 298 times
1
RFZ
- 16,814
-
What part specifically are you are having trouble with? – Matthew Cassell Nov 22 '15 at 13:27
-
@Mattos, I understand all details. He get limit function (Dirichlet function) which is discontinuous everywhere and is not integrable by Riemann. But I can't understand sequence of functions ${f_m(x)}_{m=1}^{\infty}$ is continuous or not? – RFZ Nov 22 '15 at 13:30
-
Are you asking which idea this is supposed to be a counterexample to? That would require context from the book. My best guess is that, even though the functions themselves are continuous, the pointwise limit is discontinuous on all of $\Bbb R$. – Ben Grossmann Nov 22 '15 at 13:32
-
1The functions $f_m$ are integrable but not continuous. – Ben Grossmann Nov 22 '15 at 13:33
-
@Omnomnomnom, For every fixed $m$ $$f_m(x) = \begin{cases} 1, & \text{if }m!x\text{ is integer} \ 0, & \text{if }m!x\text{ is not integer} \end{cases}$$. Why $f_m$ is integrable? – RFZ Nov 22 '15 at 13:40
-
2@RFZ because each $f_m$ is continuous (in fact zero) except at countably many points. – Ben Grossmann Nov 22 '15 at 13:45
-
@Omnomnomnom, Thanks a lot! :) – RFZ Nov 23 '15 at 16:51