M compact $p\in M$ , there exist $f:M-p\to M-p$ continuous bijection but not homeomorphism?

Question

Let M be a compact metric space. We know that if $ g:M\to M$ is a continuous bijection then it's a homeomorphism. But I want to know, if I have a continuous bijection $ f:M - \left\{ p \right\} \to M - \left\{ p \right\} $, then it's true that can always be extended to a continuous bijection $M\to M$ or not?

clearly I assume that $ M - \left\{ p \right\} $ it's under the restricted metric of M.

EDITED: Even knowing that M it's the one point compactification and that the open sets of M are all the open sets of M-p , and the complement of compacts of M-p , even with that I can't prove the result. Maybe it's not true. I'm not sure, if you want to use that you are welcome, and maybe it's false and I need a counterexample :/ I'll also change the name of the post

Answer 1

I will denote by $C(\omega)=\{0,1,2,\dots\}\cup\{\omega\}$ the one-point compactification of the discrete space on the countable set $\{0,1,2,\dots\}$. I.e. all points different from $\omega$ are isolated and neighborhoods of $\omega$ are precisely complements of finite subsets of $\{0,1,2,\dots\}$.
(This space is homeomorphic to the space $\{0\}\cup\{\frac1{n+1}; n=0,1,2,\dots\}$ with the topology inherited from real line. So this is simply a convergent sequence.)

Now I take $M=\{0,1\}\times C(\omega)$, where $\{0,1\}$ has the discrete topology. (I.e., $M$ is the topological sum of two copies of $C(\omega)$.) And I choose $p=(0,\omega)$.

It is easy to see that $M$ is a compact metric space.
(E.g. it is homeomorphic to $\{0,1\}\times(\{0\}\cup\{\frac1{n+1}; n=0,1,2,\dots\})$ with the topology induced by the usual Euclidean metric on $\mathbb R^2$.)
Note that every subset of $\{0\}\times C(\omega)$ is open in $M\setminus\{p\}$.

Let us define a map $f \colon M\setminus\{p\} \to M\setminus\{p\}$ by putting $$f(0,2n)=(1,2n)\\ f(0,2n+1)=(0,n)\\ f(1,n)=(1,2n+1)\\ f(1,\omega)=(1,\omega).$$

This map is bijective and continuous, but the extension $\overline f\colon M\to M$ with $\overline f(0,\omega)=(0,\omega)$ is not continuous, since the sequence $x_n=(0,2n)$ converges to $(0,\omega)$ in $M$ but $\overline f(x_n)=(1,2n)$ converges to $(1,\omega)\ne \overline f(0,\omega)$.

---

Here's my attempt to sketch the above map (the two big arrows indicate the direction in which the sequences $C(\omega)\times\{0\}$ and $C(\omega)\times\{1\}$ converge):

---

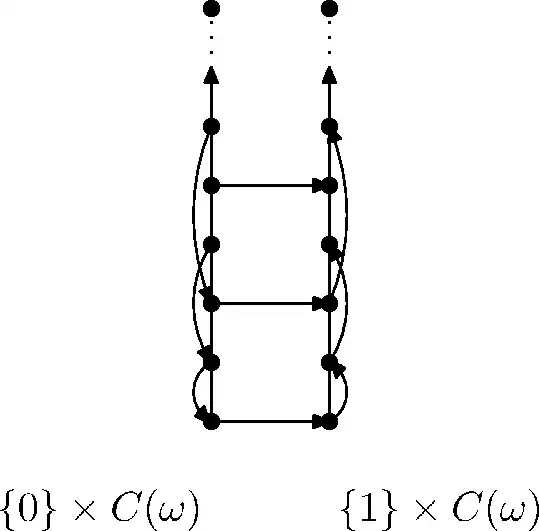
It is perhaps worth mentioning that $f^{-1}$ is not continuous. The sequence $(1,2n)$ converges to $(1,\omega)$ but $f^{-1}(1,2n)=(0,2n)$ does not converge.

So this does not contradict Theorem 29.1 from Munkres, which was mentioned in comments.

Theorem 29.1. Let $X$ be a space. Then $X$ is locally compact Hausdorff if and only if there exists a space $Y$ satisfying the following conditions:

• $X$ is a subspace of $Y$.
• The set $Y-X$ consists of a single point.
• $Y$ is a compact Hausdorff space.

If $Y$ and $Y'$ are two spaces satisfying these conditions, then there is a homeomorphism of $Y$ with $Y'$ that equals the identity map on $x$.

---

The OP indicated that he was originally thinking about the case that $M=S^n$. Since $S^n$ is the one-point compactification of $\mathbb R^n$, from Theorem 29.1 and from the fact that every continuous bijection $\mathbb R^n\to\mathbb R^n$ is a homeomorphism (which was shown in this question) we get that in the case $M=S^n$ the result from the question is true.

Answer 2

I'll add another example which I found at Ask A Topologist forum. This example is, to some extent, similar to the example above, but it might be easier to visualize.

---

I'll first put here a LaTeX-ed version of the post I linked:

This is an example of a locally compact space $S$ and a continuous bijective function $f\colon S\to S$, which is not a homeomorphism.

Let $S = \bigcup\limits_{n \in \mathbb Z} S_n \cup \{0\}$, where $S_n$ is the circle centered at the origin with radius $2^n$.
$S$ is a locally compact space as a closed subset of $\mathbb C$.
Define, for $m$ and $n$ in $\mathbb Z$, $f_{m, n} \colon S_m \to S_n$ homeomorphism (for example the multiplication by $2^{n-m}$).
Then define a bijection $g \colon \mathbb Z \to \mathbb Z$ such that $g (n) \to - \infty$ when $n \to -\infty$ and $g (n)$ is not bounded above nor bounded below when $n \to +\infty$.
For example, $g$ defined by $g (n) = n/2$ if $n$ is positive and even, $g (n) = -n$ if $n$ is positive and odd, and $g (n) = -2n$ if $n$ is negative should work.

Now, consider $f \colon S \to S$ $$ x \mapsto f_{n, g (n)} (x),\\ 0 \mapsto 0$$

$f$ is an bijection from $S_n$ to $S_{g (n)}$ for every $n$ and since $g$ is permutation of $\mathbb Z$, $f$ is a bijection from $S - \{0\}$ to $S - \{0\}$.
$f$ sends $0$ to $0$, therefore $f$ is a bijection from $S$ to $S$.
$f$ is continuous on each $S_n$, and is continuous at $0$ since $g (n) \to -\infty$ when $n \to -\infty$.
But $f^{-1}$ is not continuous at zero, because $g^{-1} (n) \not\to -\infty$ when $n \to -\infty$.

---

Now let us consider $\mathbb C\cup\{\infty\}$ as the one-point-compactification of plane.

Then we have subspace $M=S\cup\{\infty\}$.

The map $f \colon S\to S$ described above is continuous and bijective, but the extension $\overline f \colon M \to M$ such that $\overline f(\infty)=\infty$ is not continuous. To see this, just choose a sequence $(x_n)_{n=0}^\infty$ such that $x_n \in S_n$ and observe that $x_n\to\infty$ but $\overline f(x_n)=f(x_n)$ does not converge to $\infty$.

---

Interestingly, when I was Googling and trying to find similar examples online, I found the following sentence in some book:

This finishes the proof of the theorem, since every continuous bijection between locally compact Hausdorff spaces is a homeomorphism (see Theorem 10 on page 139 of [Eng68]).

It seems that [Eng68] refers to the book R. Engelking (1968). Outline of General Topology. translated from Polish. North-Holland, Amsterdam.

I only have the Polish original of this book; which of course has a different page numbering; but I did not find in the chapter on locally compact spaces anything similar to the above claim. So I guess it is a mistake or (more probably) a misquote.

Answer 3

WARNING: I just noticed there are two big problems with my answer. The closed upper half plane is not homeomorphic to the space $X$ obtained by removing an open interval from the boundary of a closed 2-disk. It is true that $X$ has a continuous self bijection which is not a homeomorphism given by folding the boundary in on itself, but $X$ is not locally compact so my example does not solve your problem. However, my link is still relevant because Jim Belk's answer on the same page exhibits a continuous self-bijection of a locally compact space.

---

As has been pointed out, the spaces obtained by subtracting a point from a compact Hausdorff space are precisely the locally compact Hausdorff spaces. So your question can be rephrased as follows.

Does there exist a continuous self-bijection of a (necessarily noncompact) locally compact Hausdorff space which is not a homeomorphism?

This is possible even for as nice a space as the upper half plane $\mathbb{H}^2 = \{ (x,y) \in \mathbb{R}^2 : y \geq 0\}$ (a manifold with boundary!).

We can also identify $\mathbb{H}^2$ with a closed 2-disk minus a point on the boundary. Or, more usefully, a closed 2-disk with an open interval subtracted from the boundary. Now there is a clear self-bijection given by tucking the boundary in on itself and this is not a homeomorphism. For a picture, see my answer here.

Are continuous self-bijections of connected spaces homeomorphisms?