3

The exterior product between blades has a relatively clear geometric interpretation: it gives the result of "extending" one factor along the other, with the direction pointing along the first factor and then the second. So the exterior product of two vectors can be imagined as the directed parallelogram between two arrows.

Is there a similar way to visualize the geometric product? Or must it just be considered algebraically?

Draconis
  • 1,443
  • 1
    Well the geometric product of two vectors yields a scaled rotation (a rotor). This is easily seen by factoring the norm out of the product: $ab = |a||b|(\cos(\theta) + i\sin(\theta))=|a||b|e^{i\theta}$ where $i$ is a unit pseudoscalar for the subspace $\operatorname{span}(a,b)$. I don't know of a geometric interpretation for the geometric product of higher dimensional blades. –  Nov 20 '15 at 00:03
  • 1
    Of course parts of the geometric product have important meanings. For instance if $A$ is a $k$-blade and $B$ is a $j$-blade where $k\lt j$, then $\langle AB\rangle_{j-k}$ is the orthogonal complement of $\operatorname{proj}BA$ in $B$. And of course $\langle AB\rangle{j+k}$ is the $j+k$-blade representing $\operatorname{span}(A,B)$ if that span is $j+k$ dimensional. –  Nov 20 '15 at 00:18
  • @Bye_World Very useful. I'm mostly looking for a general technique, but the inner product as a downward projection is a good one. – Draconis Nov 20 '15 at 05:13
  • 1
    I think the problem with finding a general geometric interpretation of the geometric product is that we don't have a general geometric interpretation of multivectors. We really only have geometric interpretations of blades and a few other convenient types of multivectors (rotors, paravectors, etc). But in general the geometric product of two blades will not be one of these special types of multivectors. –  Nov 20 '15 at 14:52
  • 2
    I think the key to developing a geometric understanding here would be to understand the geometric meaning of adding two multivectors with differently graded parts. Unless or until that happens, a general multivector will elude geometric intuition, whether it comes from a geometric product or somewhere else. – Muphrid Nov 20 '15 at 15:09

2 Answers2

3

The most intuitive interpretation of a Geometric Product I have found is from Hestenes who notes that it can be visualized as a directed arc just as a vector can be viewed as a directed line.

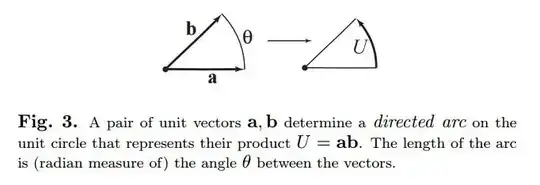
enter image description here

For more depth, see page 11 of the following:

http://geocalc.clas.asu.edu/pdf/OerstedMedalLecture.pdf

Kevin Long
  • 5,159
kieranor
  • 71
1

This is based on my answer given here: https://math.stackexchange.com/a/4304117/322997

Vectors can be thought of as representing (hyper)planes. For example, in 3D space a vector can be used to represent a plane through the origin. Now, a plane $u$ can be reflected in a plane $v$ using

$$ v[u] = -vuv^{-1}, $$

where the minus sign is needed such that when you reflect $v$ in itself, the front and back of the mirror flip ($v[v] = -v$). If we now also perform a reflection in a second plane $w$, we get the rotation

$$ w[v[u]] = (wv)u v^{-1} w^{-1} = (wv) u (wv)^{-1} $$

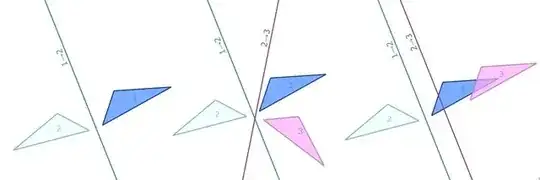
The composition of two reflections $wv$ is called a bireflection, and could in fact be either a rotation, translation, or a boost. The picture below shows how two intersecting reflections form a rotation, while parallel reflections form a translation.

enter image description here

So the product of two vectors is a bireflection. The "apples and oranges" of scalar plus bivector only appear because in order to actually compute it, we would have to somehow choose a basis. Staying with the 3D example, we could choose an orthogonal basis $e_1, e_2, e_3$ such that $e_i e_j = \delta_{ij} + e_{ij}$ and represent any plane as $x = \sum_i x^i e_i$.

Now, when we compute the bireflection $wv$ we will get a scalar and bivector part: $$ w v = \sum_{ij}(w^i e_i) (v^j e_j) = \sum_i w^i v^i + \sum_{i \neq j} w^iv^j e_{ij}. $$

So just remember the truth: there are no apples and oranges. This works in any number of dimensions: the vectors of a geometric algebra $\mathbb{R}_{p,q,r}$ form the reflection group $Pin(p,q,r)$. For more detail on this approach I would refer to this video, or to the Graded Symmetry Groups paper. Full disclaimer: I'm one of the authors.

tBuLi
  • 153
  • "The 'apples and oranges' of scalar plus bivector only appear because in order to actually compute it, we would have to somehow choose a basis." No, if I'm understanding correctly then this is false. The $k$-vector part of any multivector is basis-independent, so in particular the scalar and bivector parts of your bireflection are basis-independent, intrinsic quantities. – Nicholas Todoroff Nov 20 '23 at 17:26