1

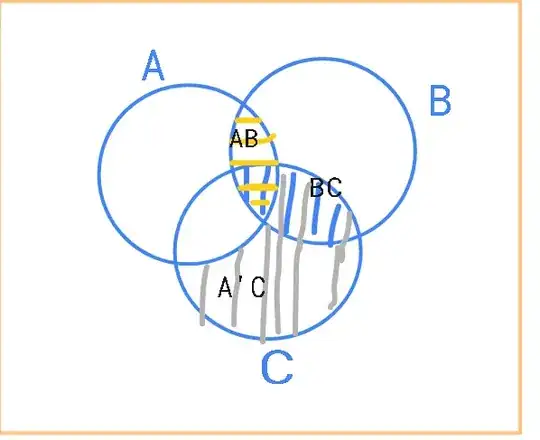
I'm trying to simplify this boolean expression:

$$(AB)+(A'C)+(BC)$$

I'm told by every calculator online that this would be logically equivalent:

$(AB)+(A'C)$

But so far, following the rules of boolean algebra, the best that I could get to was this:

$(B+A')(B+C)(A+C)$

All of the above are logically equivalent (I've made a truth table for each) but I don't understand what steps am I missing trying to simplify the expression.

I also couldn't find an "expression simplifier" tool online that could show me the steps that I'm missing.

Help / directions to go to would be much appreciated, thanks in advance.

Kevin Zakka
  • 1,544
shaqed
  • 475

5 Answers5

2

Well, clearly there's either $A$ or $A'$ in the first two terms, so use this to split the third wheel up, and absorb the pieces.

$\begin{align}(AB)+(A'C)+(BC) & = (AB)+(A'C)+(A+A')(BC) \\ & = (AB)+(A'C)+(ABC)+(A'BC) \\ & = (AB+ABC)+(A'C+A'BC) \\ & = (AB)(1+C)+(A'C)(1+B) \\ & = (AB)+(A'C)\end{align}$

Graham Kemp
  • 129,094
  • That was really helpful.. thanks! one question - could I have made it if I hadn't added any external (even though completely valid) literals like you did with (A+A') ? – shaqed Nov 17 '15 at 22:52
  • 1
    No, it seems not, @shaqed . Sometimes you do have to make things seem more complex before you can reduce them. Moving around a blockage may require taking one step back before two steps forward. – Graham Kemp Nov 17 '15 at 23:06
1

I would like to add the following explanation to the above answers:

The first two terms translate as “If A, then B, else C ”. Notice, therefore, that B and C cannot
simultaneously coexist, meaning that the third term can be safely ignored or omitted, since it
is superfluous or redundant.

Lucian
  • 48,334
  • 2
  • 83
  • 154
0

This is known as the consensus rule.

$BC$ is the "consensus" term of $AB$ and $A'C$ and can be removed or added to the boolean expression.

Derivation $$(X.Y)+(X'.Z)+(Y.Z)$$ $$=(X.Y)+(X'.Z)+(X+X')(Y.Z)$$ $$=(X.Y)+(X'.Z)+(X.Y.Z)+ (X'.Y.Z)$$ $$=(X.Y)+(X.Y.Z)+(X'.Z)+(X'.Y.Z)$$ $$=X.Y(1+Z) + X'.Z(1+Y)$$ $$=X.Y + X'.Z$$

Thus $$(X.Y)+(X'.Z)+(Y.Z)= X.Y + X'.Z$$

Kevin Zakka
  • 1,544
0

$$\begin{align*} AB+A'C+BC&=AB(C+C')+A'C(B+B')+BC\\ &=ABC+ABC'+A'BC+A'B'C+BC\\ &=(A+A')BC+BC+ABC'+A'B'C\\ &=BC+BC+ABC'+A'B'C\\ &=BC+ABC'+A'B'C\\ &=(A+A')BC+ABC'+A'B'C\\ &=ABC+A'BC+ABC'+A'B'C\\ &=AB(C+C')+A'(B+B')C\\ &=AB+A'C \end{align*}$$

Brian M. Scott
  • 616,228
0

Though this has already some good answer, I know an interesting way to look at boolean expression with less than 4 elements(for greater than 3 it becomes messy ),it might be helpful for any future user struggling with a similar problem.

Imagine them as Venn diagrams, draw their intersection using the given expression, after this most of the time question becomes trivial.

You can easily see/confirm A'C +AB covers the colored region completely.

(ignore my drawing skills) ignore my drawing skills

Dhruv Joshi
  • 100