10

How do I estimate the error for the sum of reciprocals of square roots. From calculus we know that:

$$ \int_0^n \sqrt{x} \, dx = \frac{2}{3} x\sqrt{x} \;\;\Bigg|_{x=0}^{x=n} = \frac{2}{3}n\sqrt{n}$$

I forget the name - midpoint rule, trapezoid rule ?? - basically we want to approximate the integral as a Riemann sum. How do we estimate the error?

$$ \left(1 + \sqrt{2} + \sqrt{3} + \dots + \sqrt{n} \right) - \frac{2}{3} n \sqrt{n}$$

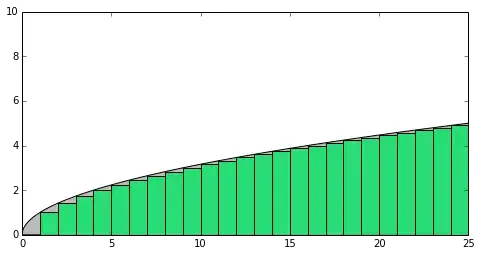
To give you a sense of how much we are losing on this approximation, let's draw two pictures.

enter image description here enter image description here

We are losing all the gray stuff in our approximation, which is quite a lot! I don't really care about the integral, what's important is the difference between all the stuff we are adding and square root of $n$.

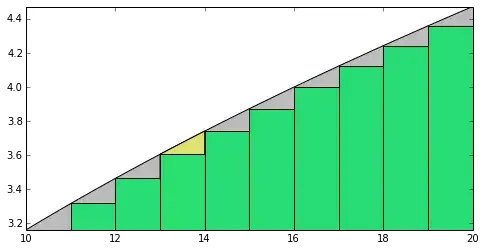
The yellow triangle has base $1$ and height $\sqrt{14} - \sqrt{13}$ so the area is:

$$ A = \frac{1}{2} \times b \times h = \frac{1}{2} \times 1 \times (\sqrt{\color{#E0E070}{14}} - \sqrt{\color{#E0E070}{13}}) = \frac{1}{2}(\sqrt{n+1} - \sqrt{n}) \approx \frac{1}{4 \sqrt{n}}$$

This suggests the total of all errors is about $\propto \sqrt{\color{#D22}{n}}$ which is not a small amount. Can anyone get the constant of proportionality?

The Euler-Maclaurin machine does crank out such error estimates, but the square root function is not so strange. Can we derive such an estimate in this specific case using basic standard inequalities?

cactus314
  • 24,438

2 Answers2

4

A trapezoidal rule gives a much better approximation: $$\sum_1^n i^{1/2}\approx \frac 1 2(f(1)+f(n))+\int_1^n f(x)\,dx= \frac 1 2 +\frac 1 2 \sqrt n +\frac 2 3 n^{3/2}-\frac 2 3$$ which recovers the biggest component of the error and ends up with an error bound by a small constant. Error analysis can also improve the above estimate to $$\sum_1^n i^{1/2}=\frac 2 3n^{3/2}+\frac 1 2n^{1/2}-\frac 1 6-\frac 1 {24}+\frac 1{24}n^{-1/2}+E_n$$ where non-negative $E_n$ is tiny ($<5\cdot 10^{-4}$).

A.S.
  • 4,004
  • Indeed, if we add up the area of the $\color{#20E070}{\text{green}} $ rectangle and the $\color{#E0E070}{\text{yellow}}$ triangle, we do get a trapezium, whose area is $A = \frac{1}{2} \times b \times (h_1 + h_2)$. – cactus314 Nov 16 '15 at 18:03
  • 1
    @cactus Simple error analysis also shows that simply subtracting $\frac 1 {12}f'(1)=\frac 1{24}$ from the above estimate will recover most of the constant error term (error of less than $4.5\cdot 10^{-4}$ from the correct constant). – A.S. Nov 16 '15 at 18:33
  • my question was originally about $\sum \frac{1}{\sqrt{n}}$ but I simplified it to $\sum \sqrt{n}$ after I drew the wrong charts :-P for me the surprise is how accurate I can get my answer without using any calculus at all. there are many result of this kind where I could try to use the same principle. Thank you. – cactus314 Nov 16 '15 at 19:46
  • @cactus Can't avoid calculus if you integrate to approximate a sum ;). – A.S. Nov 16 '15 at 20:05
  • I am also pointing out a typo in your response... you say $\sum i^{\color{red}{-}1/2}$ you should take out the minus sign. – cactus314 Nov 16 '15 at 20:06
3

Using the Binomial Theorem, we get $$ \begin{align} k^{3/2}-(k-1)^{3/2} &=k^{3/2}\left[1-\left(1-\frac1k\right)^{3/2}\right]\\ &=k^{3/2}\left[\frac3{2k}-\frac3{8k^2}-\frac1{16k^3}+O\left(\frac1{k^4}\right)\right]\\ &=\frac32k^{1/2}-\frac38k^{-1/2}-\frac1{16}k^{-3/2}+O\left(k^{-5/2}\right)\tag{1} \end{align} $$ and $$ \begin{align} k^{1/2}-(k-1)^{1/2} &=k^{1/2}\left[1-\left(1-\frac1k\right)^{1/2}\right]\\ &=k^{1/2}\left[\frac1{2k}+\frac1{8k^2}+O\left(\frac1{k^3}\right)\right]\\ &=\frac12k^{-1/2}+\frac18k^{-3/2}+O\left(k^{-5/2}\right)\tag{2} \end{align} $$ and $$ \begin{align} k^{-1/2}-(k-1)^{-1/2} &=k^{-1/2}\left[1-\left(1-\frac1k\right)^{-1/2}\right]\\ &=k^{-1/2}\left[-\frac1{2k}+O\left(\frac1{k^2}\right)\right]\\ &=-\frac12k^{-3/2}+O\left(k^{-5/2}\right)\tag{3} \end{align} $$ Combining $(1)$, $(2)$, and $(3)$ gives $$ \begin{align} &\small\left(\frac23k^{3/2}+\frac12k^{1/2}+\frac1{24}k^{-1/2}\right)-\left(\frac23(k-1)^{3/2}+\frac12(k-1)^{1/2}+\frac1{24}(k-1)^{-1/2}\right)\\[6pt] &\small=k^{1/2}+O\left(k^{-5/2}\right)\tag{4} \end{align} $$ Summing, we get that $$ \sum_{k=1}^nk^{1/2}=\frac23n^{3/2}+\frac12n^{1/2}+C+\frac1{24}n^{-1/2}+O\left(n^{-3/2}\right)\tag{5} $$ where $C=\zeta\left(-\frac12\right)=-0.207886224977354566\dots$

Why $\boldsymbol{\zeta\left(-\frac12\right)}$?

We can rewrite the reasoning given in this answer, which uses the Euler-Maclaurin Sum Formula, but use the Binomial Theorem, as above. However, the argument is exactly the same. That is, $$ \lim_{n\to\infty}\left[\sum_{k=1}^nk^{-z}-\frac1{1-z}n^{1-z}-\frac12n^{-z}\right] $$ converges uniformly to an analytic function for $\mathrm{Re}(z)\gt-1$. For $\mathrm{Re}(z)\gt1$, this function is easily seen to be $\zeta(z)$.

By analytic continuation, we get that this function is $\zeta(z)$ for $\mathrm{Re}(z)\gt-1$. For this question, plug in $z=-\frac12$.

Community
  • 1
robjohn
  • 345,667
  • I've removed the usage of Euler-Maclaurin. – robjohn Nov 16 '15 at 20:59
  • This doesn't look right. You've lost much the precision in $(1)$ (for example for $k=1$). How do you go from $(4)$ to $(5)$? You can't sum $O(k^{-5/2})$ for $k=1,..,n$ to get $O(n^{-3/2})$. This reasoning would only apply if we needed $\sum_k^N i^{1/2}$ for large $k$ and hence summed $(4)$ from $k$ to $N$ – A.S. Nov 17 '15 at 00:08
  • Where do you think I've lost precision? If $\left|a_k\right|\le Ak^{-5/2}$, then $\left|C-\sum\limits_{k=1}^na_n\right|=\left|\sum\limits_{k=1}^\infty a_n -\sum\limits_{k=1}^na_n\right| \le\frac23An^{-3/2}$. This even agrees with the Euler-Maclaurin result. – robjohn Nov 17 '15 at 00:58
  • @A.S.: This means that $\sum\limits_{k=1}^na_n=C+O\left(n^{-3/2}\right)$. Remember that we can compute $\sum\limits_{k=1}^\infty a_n$ since $\left|a_n\right|\le An^{-5/2}$. – robjohn Nov 17 '15 at 01:07
  • @A.S.: note that $(4)$ is in the form $g(k)-g(k-1)=f(k)$. Telescoping the sum says that $\sum\limits_{k=1}^nf(k)=g(n)-g(0)$. This gives $(5)$. – robjohn Nov 17 '15 at 01:14
  • Plug $k=1$ into $(1)$. You'll get $1=1\frac 1{16}+O(1)$. You lost $1/16$th. I just fail to see how you can go from $(4)$ to $(5)$ (I see that its telescoping but the error terms can't be simply added to $O(n^{-3/2})$) and especially how $C$ jumps out... – A.S. Nov 17 '15 at 01:15
  • @A.S.: I think you're looking at this all wrong. It is fairly obvious that $(1)$-$(3)$ imply $(4)$. Thus, $$\small\left(\frac23k^{3/2} +\frac12k^{1/2} +\frac1{24}k^{-1/2}\right) -\left(\frac23(k-1)^{3/2} +\frac12(k-1)^{1/2} +\frac1{24}(k-1)^{-1/2}\right) -k^{1/2}$$ is $O\left(k^{-5/2}\right)$. We can compute the sum from $k=1$ to $\infty$ (that is a well defined constant) and subtract the sum from $k=n+1$ to $\infty$ which we know is $O\left(n^{-3/2}\right)$. – robjohn Nov 17 '15 at 01:24
  • I have to go for a while. I can continue this later. – robjohn Nov 17 '15 at 01:24
  • I see. How does that sum from $1$ to $\infty$ work out to $\zeta(-\frac 1 2)\approx -0.2$? Without knowing that, we just know that $C$ is a constant (possibly a huge one - that's the consequence of what I meant by "loss of precision" in my reverse way of thinking about summing). Is there some intuitive way to think about $\zeta(x)$ for $x\le 1$? To me, the fact that the sum of the errors adds up to small $C$ is equivalent to (symbolically on the left) $\sum_1^\infty i^{1/2}\approx -0.2$ and not some other huge number. – A.S. Nov 17 '15 at 01:36
  • OK, I see how $\zeta(-\frac 1 2)$ pops out but to me it's simply symbolic manipulations as I don't grok the meaning analytical extension as a definition of $\zeta$. How would you compute $\zeta(-\frac 1 2)$? – A.S. Nov 17 '15 at 01:48
  • @A.S.: I can rewrite the reasoning that I gave in this answer, which uses the Euler-Maclaurin Sum Formula, using the Binomial Theorem, as I did above. However, the argument is exactly the same. That is, $$\lim_{n\to\infty}\left[\sum_{k=1}^nk^{-z} -\frac1{1-z}n^{1-z}-\frac12n^{-z}\right]$$ converges uniformly to an analytic function for $\mathrm{Re}(z)\gt-1$. For $\mathrm{Re}(z)\gt1$, this function is easily seen to be $\zeta(z)$. – robjohn Nov 17 '15 at 06:42
  • By analytic continuation, we get that this function is $\zeta(z)$ for $\mathrm{Re}(z)\gt-1$. For this question, plug in $z=-\frac12$. – robjohn Nov 17 '15 at 06:42
  • How would you compute/estimate $\zeta(-\frac 1 2)$? – A.S. Nov 17 '15 at 06:55
  • 1
    @A.S.: There are many ways to compute $\zeta(z)$. However, the way that seems most applicable to this question is to extend the approximation above to $$\begin{align}\small\sum_{k=1}^nk^{1/2} &=\tfrac23n^{3/2} +\tfrac12n^{1/2} +\zeta\left(-\tfrac12\right) +\tfrac1{24}n^{-1/2} -\tfrac1{1920}n^{-5/2} +\tfrac1{9216}n^{-9/2} -\tfrac{11}{163840}n^{-13/2}\ &\small+\tfrac{65}{786432}n^{-17/2} -\tfrac{223193}{1321205760}n^{-21/2} +\tfrac{52003}{100663296}n^{-25/2} -\tfrac{4741887}{2147483648}n^{-29/2} +O\left(n^{-33/2}\right)\end{align}$$ – robjohn Nov 17 '15 at 07:26
  • Plug in $n=10$ to get $18$ places: $$\zeta\left(-\tfrac12\right)=-0.207886224977354566$$ – robjohn Nov 17 '15 at 07:26
  • What is a different way to do it? In this question we are trying to approximate $\sum k^{1/2}$, so we should not compute the sum itself to estimate $\zeta(-\frac 1 2)$. – A.S. Nov 17 '15 at 07:30
  • 1
    We are only computing $\sqrt1+\sqrt2+\sqrt3+\dots+\sqrt{10}$ to get $\zeta\left(-\frac12\right)$ to $18$ places. With that, we can compute $\sum\limits_{k=1}^n\sqrt{k}$ very accurately for large $n$. What's the problem with that? – robjohn Nov 17 '15 at 07:41
  • @A.S.: I see you've edited your comment to ask for a different way to compute $\zeta\left(-\frac12\right)$. We can use the functional equation for the Riemann zeta function to get $$\zeta\left(-\frac12\right)=-\frac1{4\pi}\zeta\left(\frac32\right)$$ and we can compute $\zeta\left(\frac32\right)$ using the standard series: $$ \zeta\left(\frac32\right) =\frac1{1^{3/2}}+\frac1{2^{3/2}}+\frac1{3^{3/2}}+\frac1{4^{3/2}}+\dots $$ However, this will take a lot more work to get $18$ places. – robjohn Nov 17 '15 at 08:03