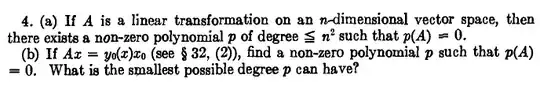2

enter image description here

Here $x_0$ is a fixed vector and $y_0$ is any linear functional.

(a) The space of all linear transformations $V \to V$ has dimension $n^2$. Consider $I,A,A^2,A^3,.....A^{n^2}$. Then this collection forms a linearly dependent set. So we have a non trivial relation amongst these which will give us a polynomial such that $p(A)=0$.

(b) Don't know how to proceed.

Marc van Leeuwen
  • 115,048
RagingBull
  • 891
  • https://en.wikipedia.org/wiki/Cayley%E2%80%93Hamilton_theorem – R.N Nov 16 '15 at 07:11
  • Use Cayley-Hamilton theorem. – Kushal Bhuyan Nov 16 '15 at 07:12
  • Cayley Hamilton theorem says that the characteristic polynomial is an annihilating polynomial. But how do we explicitly find such a polynomial in part (b)? – RagingBull Nov 16 '15 at 07:18
  • I've closed this as a duplicate, because question (a) is already answered, and question (b) is essentially asking for the minimal polynomial of the matrix of rank $1$ (or $0$ if one of $x_0,y_0$ is zero; the minimal polynomial is $X$ in that case). Summary: the minimal polynomial is $X(X-c)$ (of degree $2$) where $c=y_0(x_0)$, unless $n<2$ in which case the minimal polynomial is just $(X-c)^n$, of degree $n$ (I included the case $n=0$). There is no exception for $c=0$. See also Matrices of rank 1; show that $A^2=c\cdot A$ for some scalar $c$. – Marc van Leeuwen Nov 17 '15 at 16:12

0 Answers0