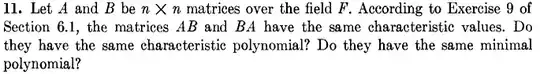2

For the second question I think the answer is no. The reason being, if we take any polynomial f and evaluate f(AB) and f(BA) then one of them being zero would not imply that the other would be zero as well. But how do I make this rigorous?

For the first part I do not know how to proceed.Perhaps I should find a counterexample?

enter image description here

RagingBull
  • 891
  • 1
    What is the relationship between the characteristic values and the characteristic polynomial? As for the second question, I think you've found a good approach. – Greg Martin Nov 15 '15 at 00:41

1 Answers1

1

Hint: For the first question, if $A$ is invertible, use the fact that $AB=A(BA)A^{-1}$. If $A$ is not invertible, approximate it by invertible matrices (if you are over an arbitrary field, you can reduce to the case of $\mathbb{C}$ by the trick discussed in the second paragraph here). For the second question, try to find some simple matrices $A$ and $B$ such that $AB=0$ but $BA\neq 0$.

Community
  • 1
Eric Wofsey
  • 330,363