2

I know that cos is even while sin is odd, and I know $\cos(\pi)=\sin((\pi/2)-x)$, but I still can't figure the derivation of $\sin (a+b)$ from $\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$. Could you give me any hint?

EA304GT
  • 1,061
CoolKid
  • 2,738
  • This can be proven easily from Euler's Formula. $e^{i \theta} = cos(\theta) + isin(\theta)$ – MadScientist Nov 14 '15 at 23:28
  • Does it really derive the formula for sine from the formula for cosine? – Bernard Nov 14 '15 at 23:30
  • @Bernard You could frame it that way, but I suppose it's sort of a cheat to do so. You could start by defining sin, cos and e^x all in terms of the taylor series. He's probably looking for a more elementary proof, but this one deserves to be mentioned because its so simple. – MadScientist Nov 14 '15 at 23:33

3 Answers3

6

$$\sin(a+b)=\cos\left(\left(\frac{\pi}{2}-a\right)+(-b)\right)=\cos\left(\frac{\pi}{2}-a\right)\cos(-b)-\sin\left(\frac{\pi}{2}-a\right)\sin(-b)\\=\sin(a)\cos(-b)-\cos(a)(-\sin(b))=\sin(a)\cos(b)+\cos(a)\sin(b)$$

Element118
  • 3,753
4

A very short hint:

Deriving ;o)

and some details:

Start from $$\cos(a+b)=\cos a \cos b-\sin a\sin b$$ and differentiate w. r. t., say, $a$: $$-\sin(a+b)=-\sin a\cos b-\cos a \sin b.$$

Bernard
  • 175,478
  • Is it so elliptic? – Bernard Nov 14 '15 at 23:36
  • What is ;o) supposed to mean? –  Nov 14 '15 at 23:46
  • Bernard was just noting the humor that the OP was using "derive" in the colloquial sense of "figure out," but that coincidentally "take the derivative of" is a good way to do so. – Simpson17866 Nov 14 '15 at 23:47
  • @Simpson17866 That's not the colloquial way of using derive, that is the "official way". As a matter of fact, using "derive" to mean "differentiate" isn't quite right. Either way I don't think this answer is useful, -1 –  Nov 14 '15 at 23:51
  • http://math.stackexchange.com/questions/80517/can-the-word-derive-be-used-to-mean-take-the-derivative-of –  Nov 14 '15 at 23:52
  • 1
    Sure, that piece of technical information was good to know and I'm surprised that I'd missed it for this long, but does the fact that a pun is not "technically" correct mean that the pun is "wrong"? If I said "I used to be a banker, but I lost interest," would the play on the word "interest" be a point in favor of the pun or a point against? – Simpson17866 Nov 14 '15 at 23:59
  • 1
    In my opinion, it'd be a point in favour of the pun… – Bernard Nov 15 '15 at 00:01
  • I don't want to discuss puns. I'm just saying that I as a person with a degree in mathematics couldn't make sense of a cryptic word and three symbols. A person that is struggling with trig is less likely than me to understand and the original answer should have been a comment at best. Since details have been filled in I changed the -1 to +1. –  Nov 15 '15 at 01:27
  • @avid19: Hints, in my mind, are written to make people think, not to give the answers. And my education – certainly very old style – taught me that sometimes, to say more, you have to say less. The most striking example I can give is a sentence by the Latin writer Suetonius which was the starting point of the classical French tragedy Bérénice (the story of the Roman emperor Titus and the Jewish princess Berenice), which is all contained in this very short sentence: Invitus invitam dimisit ([He] sent her back against his will, against her will). – Bernard Nov 15 '15 at 01:52
  • I have no issues with hints. I use them too. However I think hints should be decipherable. A single, incorrectly used word does not fall under that umbrella. However your answer is totally okay to me now so the conversation is irrelevant. :) –  Nov 15 '15 at 07:43
  • @avid The three cryptic sumbols are called a smiley. I don't know what's Bernard mother tongue, but at least in french, "differentiate" is said "dériver", hence a possible translation mistake (see the first comment of the question you refer to). Since differentiating yields the derivative, even if wrong, it should be understandable (at least to me it was, but maybe I'm biased, since I'm french). – Jean-Claude Arbaut Nov 15 '15 at 22:35
  • @avid By the way, I don't think MSE users can be expected to write a perfect english. This is the most widespread language on earth. The downside is, it's also the most victim of bad usage. – Jean-Claude Arbaut Nov 15 '15 at 22:38
4

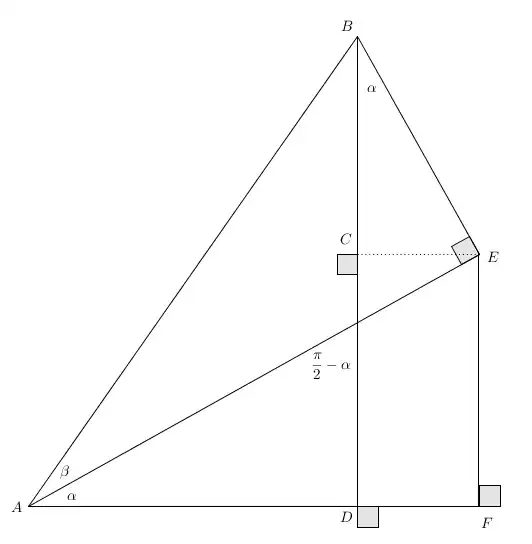
Since Element118 has already given what you expected, here is a geometric proof (the grey squares represent right angle).

trig_form

By definition, we know that $$\sin(\alpha+\beta)=\frac{|BC|+|CD|}{|AB|}=\frac{|BC|}{|AB|}+\frac{|CD|}{|AB|}$$

We want $$\cos(\alpha)\sin(\beta)+\cos(\beta)\sin(\alpha)$$

We have $\cos(\alpha)=\frac{|BC|}{|BE|}$ and $\sin(\beta)=\frac{|BE|}{|AB|}$ and it gives: \begin{equation*} \frac{|BC|}{|AB|}=\frac{|BC|\cdot|BE|}{|AB|\cdot|BE|}=\underbrace{\frac{|BC|}{|BE|}}_{\cos(\alpha)}\underbrace{\frac{|BE|}{|AB|}}_{\sin(\beta)} \end{equation*} We repeat this for $\frac{|CD|}{|AB|}$ and we get

\begin{equation} \sin(\alpha+\beta)=\cos(\alpha)\sin(\beta)+\cos(\beta)\sin(\alpha) \end{equation}

MoebiusCorzer
  • 3,284