6

Q) A circle $C_{1}$ is drawn having point P on x-axis as its centre and passing through the centre of the circle $C:x^2 +y^2=1$. A common tangent to $C_{1}$ and $C$ touches the circles at Q and R respectively . Then $Q(x,y)$ always satisfies $x^{2}=\lambda $ , then find $\lambda$ ?

Attempt

Let $(p,0) $ be the centre of $C_1$ then we have $C_1 = x^2 +y^2 -2px=0$.

Let $R=(x_1 ,y_1 )$ and $Q=(x_2 , y_2 )$

Then I wrote the equation of tangents of both circles and equated them and got

$\frac{1}{p}=x_1 + x_2$

How do I proceed? Hints?

Sujith Sizon
  • 1,138
  • What is meant by a common tangent to both circles? – Nicholas Nov 13 '15 at 09:41
  • 2
    @Nicholas a line which would intersect both circles $C_1 $ and $C$ at one and only one point respectively on each of them (i think ) – Sujith Sizon Nov 13 '15 at 09:47
  • The two circles have two common tangents symmetric to the line through the centers. You may need to review your calculation. – Quang Hoang Nov 13 '15 at 11:58
  • @QuangHoang yes i know there will be two more points but if i use slope equation of tangents and write both of them then $m(slope)$ will be unknown , how do i get around this ? – Sujith Sizon Nov 13 '15 at 12:03

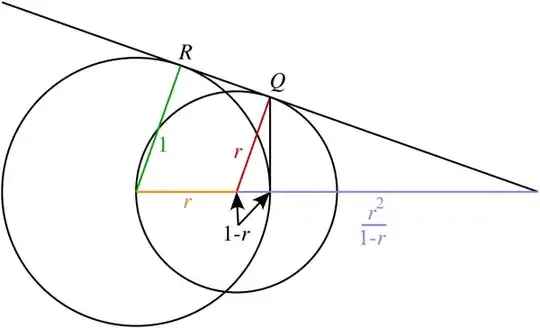
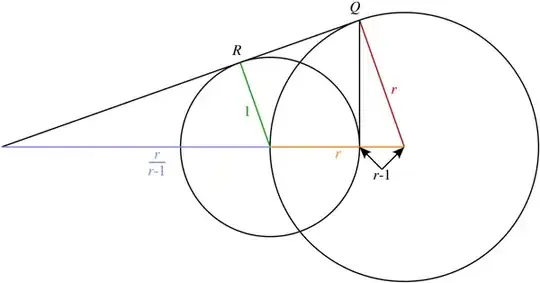
  • "common tangent to C1C1 and CC intersects the circles at Q and R" i think this would be better worded as > "common tangent to C1C1 and CC touches the circles at Q and R". The intersects word is inappropriate imo.

     – Gaurang Tandon Nov 13 '15 at 15:59
  • Please specify the tangent as it can be drawn from above or below the circles so we will have 2 sets of points where 2 tangents meet the circles. – Archis Welankar Nov 13 '15 at 16:01
  • @ArchisWelankar ..... Then $Q(x,y)$ always satisfies $x^{2}=\lambda $ .... – Sujith Sizon Nov 13 '15 at 16:04
  • @GaurangTandon i noticed that too while typing the question but refrained to edit it as i thought something deep was involved here . – Sujith Sizon Nov 13 '15 at 16:06
  • @SujithSizon I don't find anything deep here. A tangent, by definition, is a line which touches a circle at only one point, and doesn't intersect at all. – Gaurang Tandon Nov 13 '15 at 16:58
  • @GaurangTandon okay i will edit – Sujith Sizon Nov 13 '15 at 16:59

2 Answers2

5

$\boldsymbol{r\lt1}$

Using similar triangles, we get the $x$-coordinate of $Q$ to be $r+(1-r)=1$.

enter image description here

The sum of the orange and lavender segments times $r$ should be the length of the lavender segment; that is, $$ \frac{\color{#C00000}{r}}{\color{#00A000}{1}}(\color{#FF8000}{r}+\color{#8080FF}{x})=\color{#8080FF}{x} $$ solving gives $$ x=\frac{r^2}{1-r} $$

$\boldsymbol{r\gt1}$

Using similar triangles, we get the $x$-coordinate of $Q$ to be $r-(r-1)=1$.

enter image description here

The sum of the lavender and orange segments should be $r$ times the length of the lavender segment; that is, $$ \color{#8080FF}{x}+\color{#FF8000}{r}=\frac{\color{#C00000}{r}}{\color{#00A000}{1}}\color{#8080FF}{x} $$ solving gives $$ x=\frac{r}{r-1} $$

If the center of $C_1$ is on the left of $(0,0)$, then the $x$-coordinate of $Q$ will be $-1$.

robjohn
  • 345,667
1

Slope form of tangent equation of circle with centre $(a,b)$, slope $m$ and radius $r$ is: $(y-b)=m(x-h)+r\sqrt{1+m^2}$

let tangent to $C$ be: $y=mx+\sqrt{1+m^2}$

Tangent to $C_1$: $y=m(x-h)+h\sqrt{1+m^2}$

$(h,0)$ is the centre of $C_1$

Since the tangents represent the same line, $$-mh+h\sqrt{1+m^2}=\sqrt{1+m^2}$$

Solving the above equation for m, $$m=\pm\frac{h-1}{\sqrt{2h-1}}$$

I will take the plus symbol for $m$. ($\pm$ shows two such tangents are possible.)

Substituting $m$ in the the tangent equation of $C$ and rearranging, $$(y\sqrt{2h-1}+x)-h(x+1)=0$$

This is an equation of family of straight lines passing through point of intersection of lines $y\sqrt{2h-1}+x=0$ and $x=-1$ with $h$ as the parameter. It's clear that $Q$ has to be the point of intersection of the family of straight lines since that's the only point that lies on the the line for any value of $h$.

The x-coordinate of point of intersection is $-1$. So $x^2=1$.

Aditya Dev
  • 4,774