2

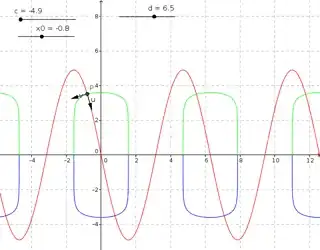
I want to find a parametric curve that would be perpendicular to all curves $y=c \sin x$

I can see that these curves will be straight lines when $x=\frac{2n+1}2\pi$ and they should become tiny circles as $x\rightarrow n\pi$, but I do not see how I would do this mathematically or what the answer would look like.

The only thing that came to my mind so far is to think of a function $F$ and equate its derivative to be $-\frac{1}{c \cos x}$

$$-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}=-\frac{1}{c \cos x}$$

$$c\cos x\frac{\partial F}{\partial x}=\frac{\partial F}{\partial y}$$

A separable solution to this would be

$$\exp \bigg(\frac{2 k \tanh ^{-1}\left(\tan \left(\frac{x}{2}\right)\right)}{c}+ky\bigg)$$

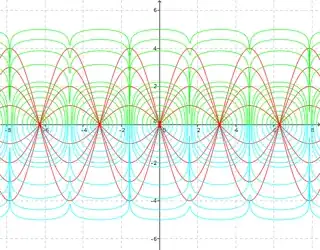
I want the parametric curves to be perpendicular for all $c$. But I do not know if this makes sense and how I would continue.

Intuitively, I am expecting to see concentric ellipses centered at $x=n\pi$

Simon S
  • 26,524
Gappy Hilmore
  • 3,937
  • I don't understand at all your lines. how can they be lines or circles for a fix value of x, i.e., a point ? – Fabrice NEYRET Nov 03 '15 at 16:32
  • 1
    the graph $y=c \sin x$ slowly evolves when you slowly change parameter $c$. I want a curve that will be perpendicular to all the graphs created by $y=c \sin x$ A straight line at $x=\pi/2$ is always perpendicular, but it is a boring solution. – Gappy Hilmore Nov 03 '15 at 16:40

1 Answers1

4

The original family is: $$ g(x, y) = \frac{y}{\sin(x)} = c $$ Implicit differentiation regarding $x$ gives: $$ \frac{y'\, \sin(x) - y \, \cos(x)}{\sin(x)^2} = 0 \Rightarrow \\ y' = \cot(x) \, y $$ An orthogonal solution must satisfy the ODE: $$ y' = - \tan(x) \, \frac{1}{y} $$ Separation of variables leads to $$ \int\! y\, dy = -\! \int\! \tan(x)\,dx \Rightarrow \\ \frac{1}{2} y^2 = \ln(\cos(x)) + C \Rightarrow \\ y = \pm \sqrt{2 \ln(\cos(x)) + d}) $$ for some integration constant $d = 2C$.

As Rahul noted, to get all solutions one must use: $$ y = \pm \sqrt{2 \ln(\lvert\cos(x)\rvert) + d}) $$ Looks like this issue.

Here is a first image:

first impression (Large version)

Here is another one:

more curves (Large version)

Community
  • 1
mvw
  • 34,562
  • 1
    Half the curves are missing, but you can get them back by taking the absolute value inside the log: $y=\pm\sqrt{2\ln\lvert\cos x\rvert+d}$. –  Nov 03 '15 at 17:30
  • @Rahul Thank you very much Rahul, that extends the solutions along the $x$-axis. Any idea how to get the curves with small "radius"? – mvw Nov 03 '15 at 17:34
  • 1
    Just take $d$ to be very small but positive. The radius is roughly $\sqrt d$. –  Nov 03 '15 at 17:37
  • Rahul: Again you seem right, thanks! I was fooled by the slider spacing I used to play around with it in GeoGebra, see the first picture. – mvw Nov 03 '15 at 17:40
  • Nice diagrams ! – Simon S Nov 03 '15 at 18:20
  • I used GeoGebra for the diagrams. The more I use it, the more I like it. – mvw Nov 03 '15 at 19:00