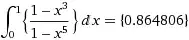An alternating series ...

Question

Find the limit of the following series:

$$ 1 - \frac{1}{4} + \frac{1}{6} - \frac{1}{9} + \frac{1}{11} - \frac{1}{14} + \cdot \cdot \cdot $$

If i go the integration way all is fine for a while but then things become pretty ugly. I'm trying to find out if there is some easier way to follow.

I assume we have $\frac 1 {5r+1} - \frac 1 {5r+4} $ - it looks like one of those cases where pairing terms might help? — Mark Bennet, May 29 '12 at 11:29
@Üstün Yıldırım: i think that we may use Mark Bennet's suggestion. — user 1591719, May 29 '12 at 11:34
Yuri noted below that you can write this sum as $1-2\sum_{k=1}^\infty\frac{1}{25k^2-1}$. There's a nice computation for that sum here — Egbert, May 29 '12 at 11:47

score 1 · Answer 1 · edited May 29 '12 at 12:21

1

$$1 - \lim\limits_{n\to\infty}\sum\limits_{i=1}^{n}{\frac{2}{(25i^2-1)}}$$

edited May 29 '12 at 12:21

Gerry Myerson

179,216

answered May 29 '12 at 11:33

Yuri Barbashov

111
1

Barbashov: nice trick. – user 1591719 May 29 '12 at 11:51
there's a typo: you should write $25i^2$ instead of $25n^2$. And it would not harm anyone if you use some words :) – Egbert May 29 '12 at 11:59
I fixed that typo. – Gerry Myerson May 29 '12 at 12:22

score 1 · Answer 2 · 2012-05-29T11:39:47.960

1

Let $S = 1 - x^{3} + x^{5} -x^{8} + x^{10} - x^{13} + \cdots$. Then what you want is $\int_{0}^{1} S \ dx$. But we have \begin{align*} S &= 1 - x^{3} + x^{5} -x^{8} + x^{10} - x^{13} + \cdots \\\ &= -(x^{3}+x^{8} + x^{13} + \cdots) + (1+x^{5} + x^{10} + \cdots) \\\ &= -\frac{x^{3}}{1-x^{5}} + \frac{1}{1-x^{5}} \end{align*}

Now you have to evaluate: $\displaystyle \int_{0}^{1}\frac{1-x^{3}}{1-x^{5}} \ dx$

And wolfram gives the answer as: enter image description here

edited May 29 '12 at 11:39

answered May 29 '12 at 11:34

i went the same way for a while, but then i got some ugly results and gave up going on. That's why i'm searching for an alternative. Thanks for your work. – user 1591719 May 29 '12 at 11:39
@Chris: Should I delete this answer. If you had written your work in the question, i wouldn't have posted this answer. – May 29 '12 at 11:40
no. Please let it here. Don't delete it. – user 1591719 May 29 '12 at 11:41

score 1 · Accepted Answer · answered May 29 '12 at 13:46

1

Below are my personal notes on a powerful method for the summation of series using complex analytic methods. The result is quite general and the final calculation is simple. If you keep this up your sleeve, later you'll come across this problem again and in Ramanujan-like fashion immediately state "The value of this sum is simply $$ \sum_{\zeta= \pm 1/5} \operatorname{Res}_{z=\zeta}\left( \frac{\pi \cot(\pi z)}{25z^2-1} \right) = \frac{\pi}{5} \cot \left( \frac{\pi}{5} \right)."$$

P.S. Sorry it isn't LaTeXed up, I don't have the stamina to type all this up at the moment.

answered May 29 '12 at 13:46

Ragib Zaman

35,127

4

Is it fair if I say I don't have the stamina to read all this at the moment? – Gigili May 29 '12 at 13:58
@Gigili lol I didn't expect that many people would, but I was hoping at least some people would scroll down to the bottom, become interesting by seeing how short and simple the final result is and think about maybe coming back to this later. – Ragib Zaman May 29 '12 at 14:06
1

@Ragib Zaman: nice. It would be great if you found a time window to LaTeX it up. – user 1591719 May 29 '12 at 14:21

An alternating series ...

3 Answers3

Linked

Related