8

Suppose that we are interested in the probability that in a set of $n$ randomly chosen people at least two people share the same birthday. We make the assumption that each day of the year (except February 29) is equally probable for a birthday. Such problem is called the birthday problem.

It seems that there are two ways to obtain this probability: $$ p(n)=1-\frac{365\cdot364\cdot\ldots\cdot(365-n+1)}{365^n} $$ and $$ q(n)=1-{365\choose n}\biggl/{365+n-1\choose n} $$ using stars and bars. When we calculate $p(n)$, the order of people is important. However, when we calculate $q(n)$, the order is not important, we can only tell how many people have a birthday on a particular day. Usually only the probability $p(n)$ is calculated.

The probability $p(n)$ is lower than the probability $q(n)$ as we see in the graph. 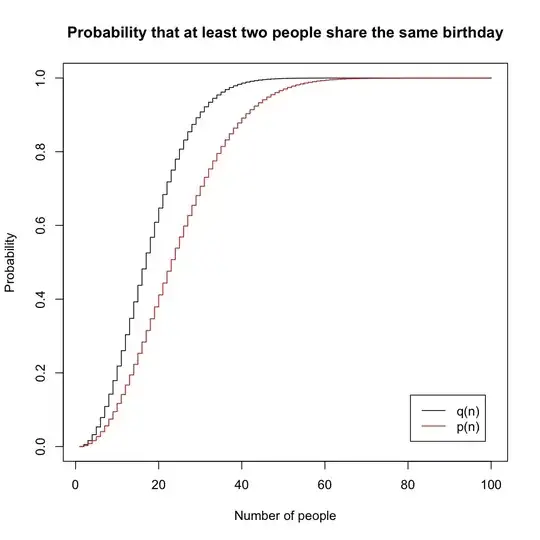enter image description here Does it make sense to calculate probability $q(n)$? How can I intuitively understand why these probabilities are different (it might seem that the importance of order should not affect the final answer)? Which one is the right way to calculate the probability in the birthday problem?

Any help is much appreciated!

Henry
  • 157,058
Cm7F7Bb
  • 17,364

1 Answers1

12

As said in the comment, in stars and bars each outcome is not equally likely.

The easiest way to see this is to evaluate $q(2)$. The stars and bars approach gives $1 - \frac{364}{366}$ which is definitely wrong.

For the simplest case, suppose you flip two coins. Represent this as two stars and 1 bar, to describe how many come up heads or tails.

$**|$

$*|*$

$|**$

The middle outcome is more likely than the others.

Titandrake
  • 306
  • 1
    Thank you for your answer (+1)! Have you got an idea how to calculate the probability using the probabilities of the outcomes when the outcomes are not equally likely? Should these two approaches yield the same answer? – Cm7F7Bb Oct 30 '15 at 20:17
  • I don't know of nice closed form expressions off the top of my head. It's possible they don't exist.

    One way you can try out is to reintroduce ordering. You can label the stars as 1,2,3,..., where you don't care about the order in a given category. So in the two coin example, it would become

    $12|$

    $1|2$

    $2|1$

    $|12$

    In general, for a specific stars and bars outcome of $n_1|n_2|n_3|...|n_k$, you need to choose $n_1$ numbers for the first category, then $n_2$ for the second, $n_3$ for the third, and so on. In principle that would give you the probability, in practice it isn't worth it.

     – Titandrake Oct 30 '15 at 20:22