Here comes the standard solution for calculating this integral. However, I suggest to have a look at Jordan's lemma, since what is below will merely be a proof of that in our specific case.
I suggest that you use the following contour for $\omega<0$:
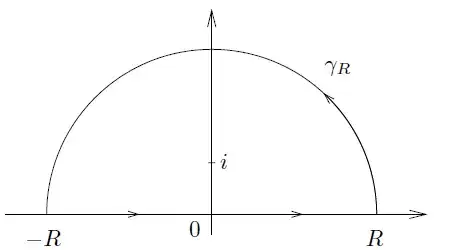
and the similar one in the lower half plane for $\omega>0$.
Let me hint on the calculation for $\omega<0$. The one for $\omega>0$ is similar, but simpler since, there is no pole. By the Residue theorem, you have
$$
\int_{-R}^R\frac{e^{-i\omega t}}{1+it}\,dt+\int_{\gamma_R}\frac{e^{-i\omega t}}{1+it}\,dt=2\pi i \,\text{Res}\,\Bigl(\frac{e^{-i\omega t}}{1+it},i\Bigr)
$$
As $R\to+\infty$, the first integral converges to what we want. The residue is easy to calculate, and I leave that to you. Let us concentrate on showing that the second integral tends to $0$ as $R\to+\infty$.
Parametrize $\gamma_R$ in the figure as
$$
t=Re^{i\theta},\quad 0<\theta<\pi.
$$
Then, since $|1+it|\geq |it|-1=R-1$, $dt=iRe^{i\theta}\,d\theta$, and
$$
|e^{-i\omega t}|=e^{\omega R\sin\theta},
$$
we find that, by the triangle inequality,
$$
\begin{split}
\biggl|\int_{\gamma_R}\frac{e^{-i\omega t}}{1+it}\,dt\biggr|&\leq
\frac{R}{R-1}\int_0^{\pi}e^{\omega R\sin\theta}\,d\theta\\
&=\frac{2R}{R-1}\int_0^{\pi/2}e^{\omega R\sin\theta}\,d\theta
\end{split}
$$
On the interval $0<\theta<\pi/2$, we have $\sin\theta>2\theta/\pi$, so the right-hand side above is bounded by
$$
\frac{2R}{R-1}\int_0^{\pi/2}e^{\omega R2\theta/\pi}\,d\theta=\frac{\pi}{(R-1)\omega}\bigl(e^{R\omega}-1\bigr).
$$
Since $\omega<0$, this expression tends to zero as $R\to+\infty$.
