2

I was thinking about this problem a few days ago and in the process I came up with what I can best describe as a two-dimensional recurrence relationship. It seemed obvious to me that this was something akin to a description of Pascal's triangle, so I began to think more carefully about a recurrence relationship that would yield the binomial coefficients. I wondered what would be the output if I tinkered slightly with the nature of the recurrence relationship.

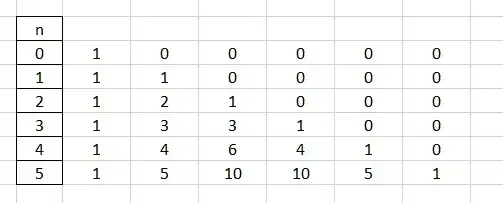
Let $t_{n,m}$ be the $m$th entry in the $n$th column of what will be a triangle like Pascal's triangle.

Example 1:

Let $t_{0,0}=1$ and let $t_{0,i}=0$ for $i \ge 1$

For $n \ge1$ let $t_{n,0}=t_{n-1,0}$ and let $t_{n,i}=t_{n-1,i}+t_{n-1,i-1}$ for $i \ge 1$

I think it's pretty obvious that $t_{n,m}$ are simply the binomial coefficients.

enter image description here

Example 2:

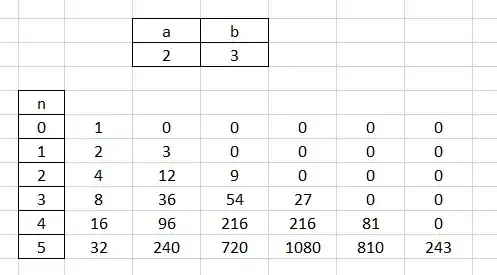
Let $t_{0,0}=1$ and let $t_{0,i}=0$ for $i \ge 1$

For $n \ge1$ let $t_{n,0}=at_{n-1,0}$ and let $t_{n,i}=at_{n-1,i}+bt_{n-1,i-1}$ for $i \ge 1$

In this case $t_{n,m}$ are the coefficients of $\left(ax+b \right)^n$.

enter image description here

So far the recurrence relationships have been what I guess you could call homogeneous. The next example is what I stumbled across in the other question.

Example 3:

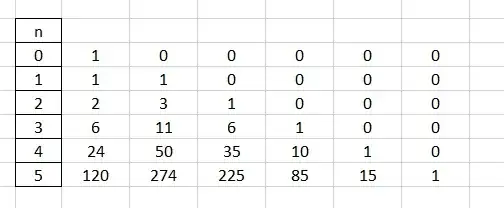
Let $t_{0,0}=1$ and let $t_{0,i}=0$ for $i \ge 1$

For $n \ge1$ let $t_{n,0}=it_{n-1,0}$ and let $t_{n,i}=it_{n-1,i}+t_{n-1,i-1}$ for $i \ge 1$

enter image description here

It's intersting to see the factorials and the triangle numbers here.

I then decided to generalise as follows:

Example 4:

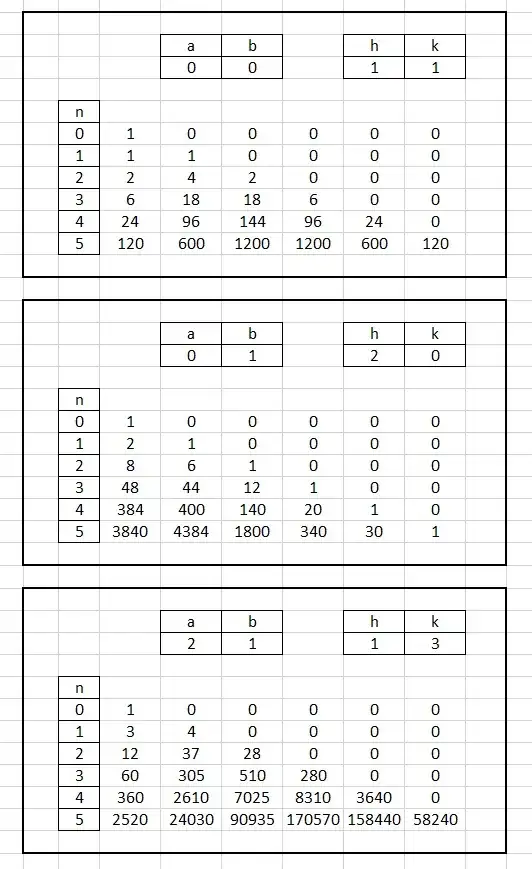
Let $t_{0,0}=1$ and let $t_{0,i}=0$ for $i \ge 1$

For $n \ge1$ let $t_{n,0}=hit_{n-1,0}$ and let $t_{n,i}=(a+hi)t_{n-1,i}+(b+ki)t_{n-1,i-1}$ for $i \ge 1$

My spreadsheet will calculate the values of $t_{n,m}$ but I now have no idea what they are!

enter image description here

To conclude, my questions are:

How can I prove that Example 1 gives the binomial coeffients?

How can I prove that Example 2 gives the coefficients of $\left(ax+b \right)^n$ ?

Can we find a way to describe $t_{n,m}$ as a function of $n, m, a, b, h, k$ ?

Is there a more general situation that has already been studied? Something like $t_{n,i}=f(i)t_{n-1,i}+g(i)t_{n-1,i-1}$

Community
  • 1
tomi
  • 9,594
  • 1
    Note that your third example is the Stirling numbers of the first kind. That the first example is the binomial coefficients is well-known, since you’re just using Pascal’s recurrence for the binomial coefficients with the same initial values, and the second follows easily from Pascal’s recurrence and the binomial theorem. – Brian M. Scott Oct 21 '15 at 23:45
  • Yes. I am happy with the first two. Stirling numbers are new to me. Thank you. – tomi Oct 21 '15 at 23:47
  • 2
    Yes, such things have been studied. A general technique is to look at a two-variable generating function, e.g. $f(x, y) = \sum f_{n, m} x^n y^m$. – Qiaochu Yuan Oct 22 '15 at 03:16

1 Answers1

-3

I have been obsessed with this "weighted Pascal's triangle" for some time now, and it has become a goal of mine to determine a formula (n p) that can give me any one of these coefficients.

1

1 1

1 3 2

1 6 11 6

1 10 35 50 24

1 15 85 225 274 120

I have located several patterns.

Farthest to the right: the factorials.

Farthest to the left: N

Second column on the left: the triangulars.

Second column on the right: the harmonic numerators, n!*Hn

I have also developed a set of formulas which give any particular coefficient of any particular column (shifted to compensate for columns previously accounted for).

Third column on the left: (n+2)(n+3)(n+4)(3n+11)/24

Fourth column on the left: (n+2)(n+3)(n+4)^2(n+5)^2/48

Fifth column on the left: (n+2)(n+3)(n+4)(n+5)(n+6)(15n^3+240n^2+1265n+2192)/5760

Sixth column on the left: (n+2)(n+3)(n+4)(n+5)(n+6)^2(n+7)^2(3n^2+35n+96)/5760

And so on...

Plug in any n into any one of these particular formulas and it'll give you whichever coefficient of the weighted Pascal's triangle that you want.

I am currently stuck at this point, for it has been my goal to determine some kind of coherent link that binds these formulas together. Preliminary calculation suggests that the denominators are quite elementary (some form of factorial), though I have not solved them yet. And the numerator has a consistent addition of a factor (n+p), so indeed there are coherent *similarities* between these formulas.

The problem is with these seemingly random odd-ball factors that make no sense to me.

If you are still enthusiastic about the aforementioned triangle, I would like to propose a friendship; I will share with you how I derived these formulas and perhaps we can figure out an explicit formula that will give any value of this triangle we choose.

Thanks, Marcus.

[email protected]

Marcus
  • 1
  • 1