The thing which you want to prove is not true. (Also it is not correctly formulated. If you write ordinal similar to the set of all functions from $b$ to $a$, you should also write some well-ordering for this set.)
The important thing here is to understand the diference between ordinal exponentiantion and cardinal exponentiation.
If $a$, $b$ are cardinals then by $a^b$ we mean the cardinality of the set of all maps from $b$ to $a$.
If $a$, $b$ are ordinals then by $a^b$ we mean an ordinal, which is usually defined in the way you described in your question.
These two things are different, e.g. $\omega^\omega$ (as ordinal power) has cardinality $\aleph_0$ which is less than $\aleph_0^{\aleph_0}=\mathfrak c$.
I don't think that there is some natural well-ordering on the set of all maps from $b$ to $a$ for ordinals $a$, $b$.
To see that cardinality of $\omega^\omega$ is $\aleph_0$ we can:
Quote from Wikipedia:
Warning: Ordinal exponentiation is quite different from cardinal exponentiation. For example, the ordinal exponentiation $2^\omega = \omega$, but the cardinal exponentiation $2^{\aleph_0}$ is the cardinality of the continuum which is larger than $\aleph_0$. To avoid confusing ordinal exponentiation with cardinal exponentiation, one can use symbols for ordinals (e.g. $\omega$) in the former and symbols for cardinals (e.g. $\aleph_0$) in the latter.
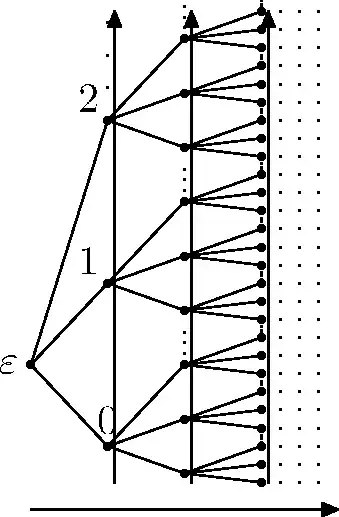
I am not sure to which extent it's useful here, but I'll add one possible graphical representation of $\omega^\omega$, since I've mentioned this ordinal a few times.
Imagine all finite sequences of non-negative integers ordered as in the picture: first from left to right (by the length) and in each column from bottom to top (lexicographically). The symbol $\varepsilon$ represents empty sequence, each point represents the sequence given by the path from root to this dot.
It should be at least clear that in the first column we have $\omega$, in the second column $\omega^2$ etc. (Since $\omega+\omega^2=\omega^2$, if we take all points up to second column, we get still $\omega^2$.) So clearly the ordinal in the picture is at least $\sup\{\omega^n; n<\omega\}$. If you think about it a little bit, you'll find out that this ordinal is the union of $\omega^n$'s, if $\omega^n$ is represented by the first $n$ columns.

$\mu_a$? – Martin Sleziak May 24 '12 at 11:12