0

enter image description here

For part i), my answer was $\begin{bmatrix}-1 & 2 & 0 \\ 2 & 5 & 1 \\0 & 1 & -5\end{bmatrix}$

But for part ii), when I try to calculate $\det(A-λI)=0$, it comes down to $-λ^3 -λ^2+29λ+45 =0$, which doesn't have a neat solution. I'm sure I've done something wrong here.

dineshdileep
  • 8,887
mathstack
  • 899
  • 2
    Your part 1 is wrong. Take a look at the diagonal entries. – dineshdileep Oct 22 '15 at 00:42
  • 1
    here is an alternative process to diagonalize a symmetric matrix $A$ without explicitly computing its eigenvalues (which in fact is the process that question (ii) is asking you to use): http://math.stackexchange.com/questions/395634/given-a-4-times-4-symmetric-matrix-is-there-an-efficient-way-to-find-its-eige/1170390#1170390

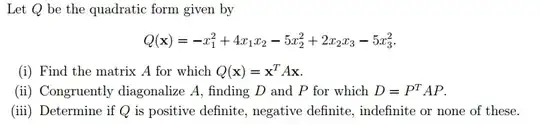
    for some theoretical details about this method, you check this post: http://math.stackexchange.com/questions/1388421/reference-for-linear-algebra-books-that-teach-reverse-hermite-method-for-symmetr

     – etothepitimesi Oct 22 '15 at 00:56

0 Answers0