I have a following series
$$ \sum\frac{1}{n^2+m^2} $$
As far as I understand it converges. I tried Cauchy criteria and it showed divergency, but i may be mistaken.
When I calculate it in matlab or Maxima it have a good behaviour and converge to finite number about 10.17615092535112.
The convergency plot is following:
Just to give an answer. The series diverges since $$\frac{1}{n^2+m^2}\geq \frac{1}{(n+m)^2}$$ and therefore $$\sum_{n,m\in\mathbb N}\frac{1}{n^2+m^2}\geq \sum_{n,m\in\mathbb N}\frac{1}{(n+m)^2}.$$ For the RHS we have $$\sum_{n,m\in\mathbb N}\frac{1}{(n+m)^2}=\sum_k\sum_{n+m=k}\frac{1}{k^2}=\sum_k\frac{k-1}{k^2}\sim\sum_k\frac{1}{k}.$$
Matlabs sum for $\displaystyle \sum_{n=1}^{10^5} \frac{1}{n}$ is actually quite spot on, it's not a fault of machine accuracy. The series is called the Harmonic series and is known to diverge very slowly. In fact, it behaves approximately like $\gamma + \ln n$ where $\gamma$ is the Euler-Mascheroni constant, about $0.57721.$ At $n=10^5$ we indeed expect about $0.57721 + 5\ln 10 \approx 12.0901.$
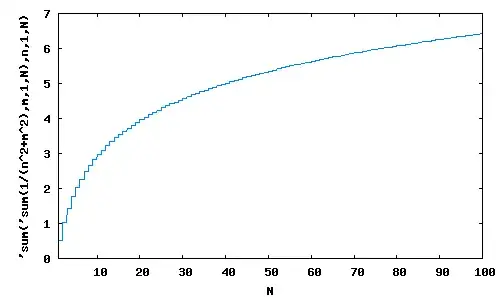
Matlab is also not saying anything incorrect for the original series, its results were just interpreted incorrectly (in a similar way to the previous example). The sum grows quite slowly. Consider if we order the sum like this: $$\sum_{m=1}^{\infty} \sum_{n=1}^{\infty} \frac{1}{m^2+n^2}.$$
By Residue Calculus methods, one can show that the inner sum is equal to $$ \frac{\pi m \coth(\pi m) -1}{2m^2}.$$
$\coth$ tends to $1$ exponentially quickly so one expects $$\sum_{m=1}^k \sum_{n=1}^{\infty} \frac{1}{m^2+n^2} \approx \frac{\pi \ln k}{2} + \frac{6\gamma \pi-\pi^2}{12}$$ for large $k.$
