Homeomorphism between real projective space with an open ball removed and the Möbius band

Question

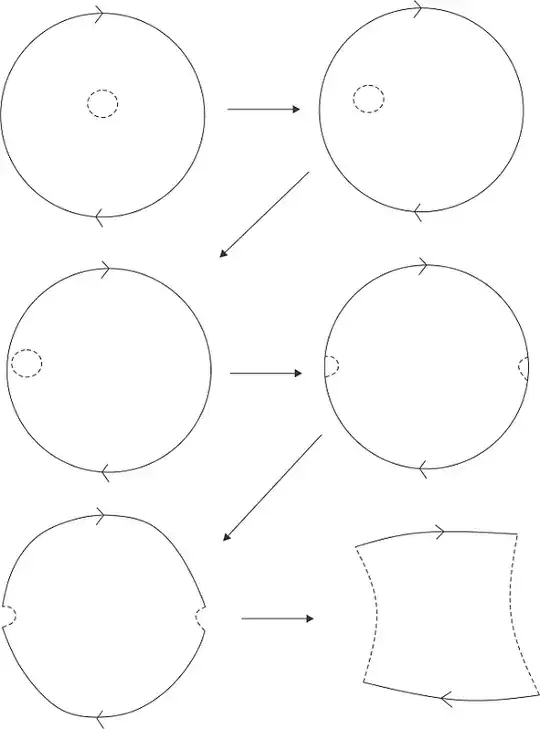
The real projective space with an open ball removed is homeomorphic to the Moöius band

How can I prove it?
Can I find the homeomorphism explicitly?

You likely have some constructions of $\Bbb RP^2$ and the Mobius band as quotients of $[0,1]^2$. Use these. — PVAL-inactive, Oct 18 '15 at 05:16

Aloizio Macedo · Answer 1 · 2015-10-18T15:41:27.977

6

Hint: (This is what PVAL means, only visually exposed:)

edited Oct 18 '15 at 15:41

answered Oct 18 '15 at 05:43

Aloizio Macedo

1

It seems that for picture 1, 2 you are removing the interior of that circle, but at 3 you seem to excluding the outside. Can you briefly explain how you go from 2 to 3? Thanks. – Oct 18 '15 at 06:04
1

When he inflates that circle he eventually approaches the edges on the top and bottom, recall since the left and right sides are connected, by translating the circle over to cutting out to the left most side it wraps over to the right side too. The exterior of this polygon is still contained in the interior of the projective plane, before the cut is made, so he is free to slide out to the exterior of the "sides" before the slice is made. But i'm curious if theres a cleaner line of reaonsing that isn't as wishy washy as what i've given – Sidharth Ghoshal Oct 18 '15 at 07:37
@JohnMa I see what you mean. I've added more intermediate pictures for clarification. – Aloizio Macedo Oct 18 '15 at 14:07

1 Answers1