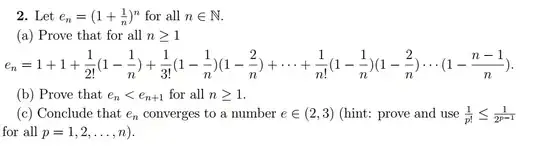proving montonity and convergence of sequence en = (1 + 1/n)^n

Question

Prove the following. What would be the summation formula be for the first part?

Answer 1

From the Binomial Theorem, we have

$$\begin{align} e_n&=\left(1+\frac1n\right)^n\\\\ &=\sum_{k=0}^n\binom{n}{k}\left(\frac1n\right)^k\\\\ &=1+n\left(\frac1n\right)+\frac{n(n-1)}{2!}\left(\frac1n\right)^2+\cdots+\frac{(n)(n-1)(n-2)\cdots(n-(n-1))}{n!}\left(\frac1n\right)^n\\\\ &=1+1+\frac1{2!}\left(1-\frac1n\right)+\frac1{3!}\left(1-\frac1n\right)\left(1-\frac2n\right)\\\\ &+\cdots+\frac1{n!}\left(1-\frac1n\right)\left(1-\frac2n\right)\cdots\left(1-\frac{n-1}n\right) \tag 1 \end{align}$$

as was to be shown!

---

To show that $e_n$ is increasing we will show that $\frac{e_{n+1}}{e_n}\ge 1$. To that end, we write

$$\begin{align} \frac{e_{n+1}}{e_n}&=\frac{\left(1+\frac{1}{n+1}\right)^{n+1}}{\left(1+\frac{1}{n}\right)^n}\\\\ &=\left(\frac{n(n+2)}{(n+1)^2}\right)^{n+1}\left(1+\frac1n\right)\\\\ &=\left(1-\frac{1}{(n+1)^2}\right)^{n+1}\left(1+\frac1n\right) \tag 2\\\\ &\ge\left(1-\frac{1}{n+1}\right)\left(1+\frac1n\right) \tag 3\\\\ &=1 \end{align}$$

where in going from $(2)$ to $(3)$, we used Bernoulli's Inequality. Thus, $e_n$ in monotonically increasing; and we are done!

---

From $(1)$ is trivial to see that $e_n\ge 2$ for $n\ge 1$.

Noting that all of the parenthetical terms are less than $1$, and $n!>2^{n-1}$ for $n\ge2$, then for $n\ge 2$, we have

$$e_n\le 1+1+\sum_{k=1}^\infty \frac{1}{2^k}=3$$

Thus, we conclude that $e_n$ is a monotonically increasing sequence that is bounded above by $3$. Therefore, $e_n$ converges to some real number betweem $2$ and $3$. And we are done!

Answer 2

To prove (a) and (b) use the binomial theorem. To prove (c) use the hint, that is, bound $e_n$ above by a geometric progression with ratio $1/2$.

Answer 3

Hint: Binomial theorem and

$$1-\frac{k}{n+1} > 1-\frac{k}{n}$$