What is $(-1)^{3/2}$?

Question

Which one is the right way?

$$(-1)^{\frac32}=(-1)^{1+\frac12}=-1\times \sqrt{-1}=-i$$

Or,

$$(-1)^{\frac32}= \left((-1)^{\frac12}\right)^{3}= i^3=-i$$

Or,

$$(-1)^{\frac32}=\left((-1)^3\right)^{\frac12}=\sqrt{-1}=i$$

Did you obtain this with Mathematica (or Wolfram Alpha) ? There is no way to tell, actually, if you do not specify more details concerning how you obtained this expression. — Tom-Tom, Oct 14 '15 at 08:16
@Tom-Tom No, neither Mathematica nor Wolfram Alpha. And it's not derived from an equation or something. — Omur, Oct 14 '15 at 08:28
@MiguelAtencia That's a complete coincidence that even the title is same. The question came to mind when solving a problem on Brilliant.org. Here is the link if you want proof: [Link] (https://brilliant.org/problems/inspired-by-sandeep-bhardwaj-p/?group=GIMZsaee9YFH) — Omur, Oct 14 '15 at 12:45

score 8 · Accepted Answer · answered Oct 14 '15 at 08:10

8

All are equally right or wrong. Exponentiation is multi-valued unless the base is a positive real, or the exponent is an integer.

As such you can only expect the usual power rules to work under the interpretation that one of the valid values of each side of the identity will be a valid value for the other.

Going by the best definition we have for this case, $$ a^b = \exp(b\cdot \log a) $$ we find that the principal value of $(-1)^{3/2}$ is $\exp(3\pi i/2)=-i$, because the principal logarithm of $-1$ is $\pi i$ rather than $-\pi i$.

answered Oct 14 '15 at 08:10

hmakholm left over Monica

286,031

Nice solution. I was wondering what the principal root would be. Thanks – Omur Oct 14 '15 at 08:32
What you write is just a convention. We can have a convention that $\mathrm i=\mathrm e^{\mathrm i\pi/2}$ or $\mathrm i=\mathrm e^{\mathrm i (k2\pi+\pi/2)}$. That would just impact the result of $\mathrm i^{\mathrm i}$ which would be either $\mathrm e^{-\pi/2}$ or $\mathrm e^{-\pi(2k+1/2)}$ for any $k\in\mathbb{Z}$. (Pick up your favorite $k$...) The problem is that the premise, i.e. writing something like $(-1)^{3/2}$ of $\mathrm i^{\mathrm i}$ has no mathematical meaning outside of context. – Tom-Tom Oct 14 '15 at 09:17
@Tom-Tom: Of course the principal value is a convention. Are you contradicting the answer or agreeing with it? – hmakholm left over Monica Oct 14 '15 at 12:11
In my opinion, your answer is not precise enough. It gives the impression that the convention applies whatever the context. I prefer this answer to a similar question (actually, it is quite the same question). – Tom-Tom Oct 14 '15 at 12:14
@Tom-Tom: Is there any context where this is not the principal value? Both the $(-\pi,\pi]$ and $[0,2\pi)$ conventions give this result. – hmakholm left over Monica Oct 14 '15 at 12:28
@HenningMakholm. You can always find a context. In that case, for instance, consider the map $f:z\mapsto z^{3/2}$ defined on ${z\in\mathbb C, \operatorname{Im}(z)\leq 0}$. – Tom-Tom Oct 14 '15 at 13:02
@Tom-Tom: I can't think of a context in which that would be called the principal value. – hmakholm left over Monica Oct 14 '15 at 13:15
My previous example requires the convention $(-2\pi,0]$. – Tom-Tom Oct 14 '15 at 13:36
@Tom-Tom: Can you reference any textbooks or other similar sources that use that convention for the principal argument? – hmakholm left over Monica Oct 14 '15 at 13:51

score 4 · Answer 2 · answered Oct 14 '15 at 08:46

Extending exponentiation to complex numbers results in the problem that you'll have to select which branch to use since solving the equation $z^n = a$ has multiple solutions.

If you keep in mind that you have to stay on the branch all the identities will still hold, but the fault (like you do) is often that this is forgotten.

In this sense you will have to start with knowing how you get to $-1$. You must have a path from a positive real number that doesn't cross the origin that ends up at $-1$, depending on that path $-1^{3/2}$ can take two different values ($i$ or $-i$).

From the first calculation one would assume that you've taken the counter clockwise path around the origin, this will result in $-1^{3/2}=-i$. Along that path you will get $\sqrt{-1}=i$ and your result is correct.

The second is the same.

But for the third, you'll get $-1^3=-1$ which the RHS is reached by going one and a half rounds round origin counter clockwise. With that path $\sqrt{-1}$ is no longer $i$, it's in fact $-i$. So the result would be $-i$ for this case as well.

On the other hand if you went clockwise to the first $-1$ you would get the third result that you indicated, but then you've got another path and you would get the same result for the first two calculations as well.

Note that this extension also applies to the positive real numbers as well. It's just that when not having complex numbers there's no way of getting this ambiguity by reaching the number along another path.

score 1 · Answer 3 · answered Oct 14 '15 at 14:54

Using the following rules, with $a,b \in \mathbb{R}$:

$\left|a^b\right|=\left|a\right|^b$;
$\arg\left(a^b\right)=\tan^{-1}\left(\cos(b\cdot\arg(a)),\sin(b\cdot\arg(a))\right)$

$$(-1)^{\frac{3}{2}}=$$ $$\left|(-1)^{\frac{3}{2}}\right|e^{\arg\left((-1)^{\frac{3}{2}}\right)i}=$$ $$\left|-1\right|^{\frac{3}{2}}e^{\arg\left((-1)^{\frac{3}{2}}\right)i}=$$ $$1^{\frac{3}{2}}e^{\arg\left((-1)^{\frac{3}{2}}\right)i}=$$ $$e^{\arg\left((-1)^{\frac{3}{2}}\right)i}=$$ $$e^{\tan^{-1}\left(\cos\left(\frac{3\pi}{2}\right),\sin\left(\frac{3\pi}{2}\right)\right)i}=$$ $$e^{\tan^{-1}\left(0,-1\right)i}=$$ $$e^{-\frac{\pi}{2}i}=$$ $$\cos\left(-\frac{\pi}{2}\right)+\sin\left(-\frac{\pi}{2}\right)i=$$ $$0+(-1)i=$$ $$(-1)i=-i$$

score 0 · Answer 4 · answered Oct 14 '15 at 08:21

Keep in mind the four quad-roots of 1: 1, -1, i and -i. Any of these, raised to the fourth power, equals 1.

If you haven't encountered the complex plane yet, it will make visualizing these types of relations much much easier. Just like the number line did when you first started learning negative numbers.

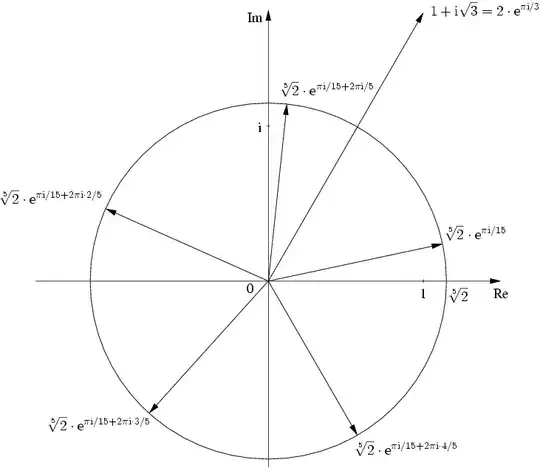
Plot a number on the complex plane, determine the counterclockwise angle from the x axis (the positive real axis) to the number you've plotted—don't actually measure the angle, but observe it—divide that angle by whatever root you're taking (3rd root -> divide the angle by 3) and you have the angle of ONE of the answers. Draw a ray from the origin through that angle, and then two other rays making for a 3-symmetrical design, and you have the angles of the other two answers.

Here is an image for fifth roots. For the purposes of understanding my description of the visualization process, the numbers on the diagram are unimportant.

Yes, I know about Argand diagram. But I think the answer you've given here is the solution of $x^{\frac23}=-1$ which is not the same. There should only be one root. — Omur, Oct 14 '15 at 08:36
No, it doesn't matter what the number is. I was just giving an example for 3rd root. For (-1)^(3/2): Start with -1, observe the angle (180 degrees), multiply by the numerator of the exponent (180 times 3 = 540 which is equivalent to 180), then divide by the denominator of the exponent (180 / 2 = 90) and add in the symmetry lines for the other answers. (2nd root means 2-symmetry, so -90). Since the magnitude of the original number is 1, that doesn't change, so the two answers are i and -i. (1 at 90 degrees and 1 at -90 degrees.) — Wildcard, Oct 14 '15 at 18:48

What is $(-1)^{3/2}$?

4 Answers4