It is pretty easy to visualize the ideals of $\mathbb{Z}$ in the "integer line".
Let's go up to $\mathbb{Z}[i]$ and consider the ideal $3\cdot\mathbb{Z}[i]$.
We can visualize it as a "sub-lattice" of the gaussian integers that contains the vertex $0+0i$ and has edges of lenght 3. This is because
\begin{equation} 3\cdot\mathbb{Z}[i]=\{(3a)+(3b)i)\:|\:a,b\in\mathbb{Z}\} \end{equation}
and so this is kind of obvious and intuitive.
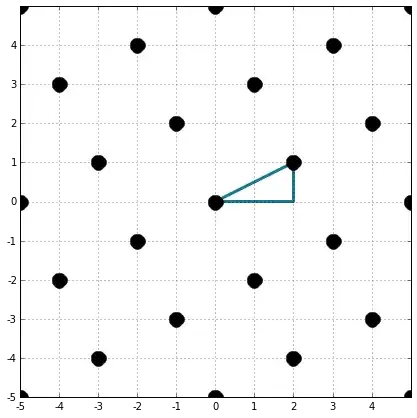
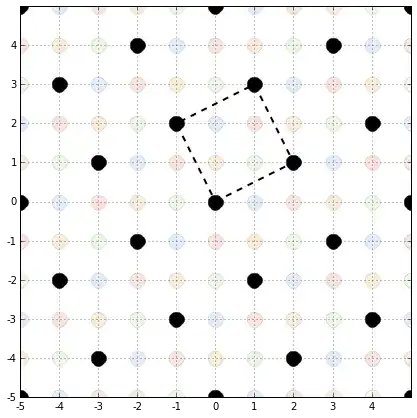
What about, for example, the ideal $(2+i)\cdot\mathbb{Z}[i]$?
We can see a copy of $5\cdot\mathbb{Z}$ inside it and also the elements of $\mathbb{Z}[i]$ lying over the line $y=\frac{1}{2}x$. Are there any others points I am missing? I think that yes, but I'm not sure how to find those.
Every element of $(2+i)\cdot\mathbb{Z}[i]$ is of the form $(2a+b)+(a+2b)i$, but is not clear to me which geometric figure we get from this. I'd appreciate if someone could explain it to me.
Thank you in advance.
Also, a small extra question: Is there any online website where I can draw things in the plane described by 2 parameters? That would answer my question, even though an algebraic explanation would be great.