The operation mathematically means $$(\nabla \times \vec A)\cdot\hat n = \lim_{\Delta S\to\ 0} \frac{\oint\vec A\cdot\ d\vec l }{\left | \Delta S \right |}$$ and the proof of this is quite logical.
In textbooks, I have found that they relate curl to rotation.
But how does the above mathematical treatment show this relation?
Any mathematical help is welcome.
Let $\bf{C}$ be any vector-field. Let there be a closed-curve $\Gamma$. Take the line-integral of $\bf C$ around this complete loop that is, take the tangential-component of the field at any point on the curve & take dot-product of $\mathbf{C}_\text{tangential}\cdot d\mathbf{s}$ & integrate over the whole loop. This is circulation : $$\text{Circulation}_{\Gamma}=\int_{\Gamma} \mathbf{ C} \cdot d\mathbf{s}.$$
Now make partitions on $C$ with an intermediary-bridge, say $B$; this then will make two loops viz; $\Gamma_1 \;\&\; \Gamma_2.$ Now circulation over the whole loop is just line-integral around each sub-loop that is, $$\text{Circulation}_{\Gamma} \\= \text{Circulation}_{\Gamma_1} + \text{Circulation}_{\Gamma_2}\\= (\text{Circulation}_{\Gamma_a} + \text{Circulation}_{\Gamma_{ab}}) + (\text{Circulation}_{\Gamma_b} -\text{Circulation}_{\Gamma_{ab}})\\ =\text{Circulation}_{\Gamma_{a}} + \text{Circulation}_{\Gamma_{b}}.$$
Break into still further smaller loops as $\Gamma_1,\Gamma_2,\Gamma_3 \ldots \Gamma_N.$
Circulation over the whole-loop $$\int_{\Gamma} \mathbf{C}\cdot d\mathbf{s}= \sum_{i=1}^N\int_{\Gamma_i} \mathbf{C}\cdot d\mathbf{s}_i.$$
Now we want to get the infinitesimal-circulation characteristic to a certain coordinate. We then make $N\to \infty;$ however each integral that is $\int_{\Gamma_i} \mathbf{C}\cdot d\mathbf{s}_i \to 0$ as $N\to \infty.$ So, in order to get the finite characteristic which is associated with circulation locally to a point, we divide each integral by the area enclosed by each sub-loop. That is, take the ratio of circulation to loop area$$\frac{\text{Circulation}_{\Gamma_i}}{a_i}.$$ This is our local-property that is the infinitesimal circulation of the vector-field at a certain point (around it) is given by $$\lim_{a_i\to 0} \frac{\int_{\Gamma_i} \mathbf{C}\cdot d\mathbf{s}_i}{a_i}.$$
jpg; hope you can see them now.
–
Oct 16 '15 at 05:33
First a small disclaimer as the rotation may not be rotation in the same sense as the question-maker intends, but anyways. Please tell me if I misunderstand the question and I can remove it.
A rotation $\phi$ radians can be described as $\left[\begin{array}{rr} a&-b\\b&a\end{array}\right], {a = \cos(\phi), b = \sin(\phi)}$, and an infinitesimal rotation in vector analysis is $$\nabla \times {\bf v} = \frac{\partial {\bf v}_x}{\partial y} - \frac{\partial {\bf v}_y}{\partial x}$$ So how do these relate to each other, or more interestingly how does $\phi$ relate to the cross product above.
An interesting thing is that the matrix operator above is in fact how the vector changes, not how it moves i.e. the additive part. To get the additive part, we need to take I minus the rotated vector, i.e. the change vector.
We need some discrete filters to measure the rotation, and here are some basic traditional Sobel filters. These are linear filters which are applied on a discretization of a function, usually on a regular cartesian grid. In mathematical terms we perform a discrete convolution with the filters
$$D_x = \left[\begin{array}{rr} 1&0&-1\\2&0&-2\\1&0&-1\end{array}\right] \hspace{1cm} D_y = \left[\begin{array}{rrr} 1&2&1\\0&0&0\\-1&-2&-1\end{array}\right]$$
This convolution is defined as $$F(i,j) = \sum_{k,l \in \{0,1,2,3\}} I(i+k,j+l)D_x(3-k,3-l)$$ and produces the filter response $F$. You can read more about linear filtering (discrete convolution) and Sobel filters in particular.
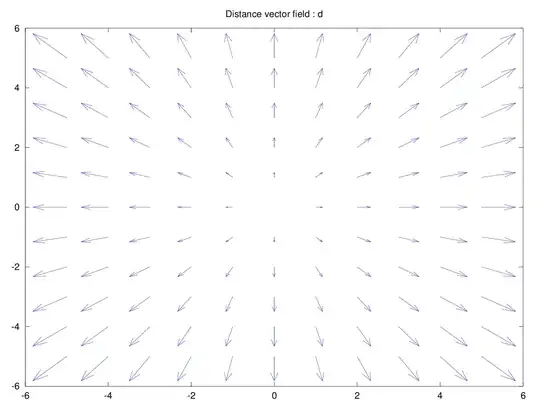Local displacement vector field. Each vector points out from the middle with the difference in coordinates.
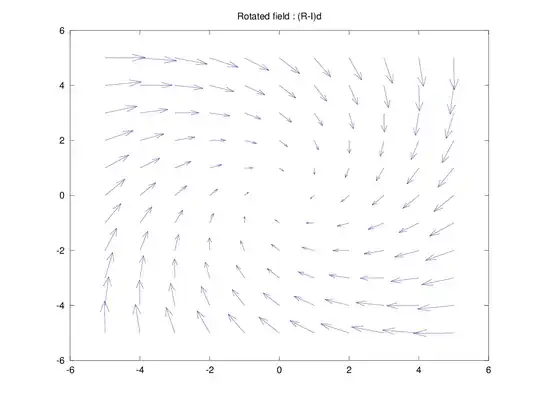
After applying the rotation described above for $\phi = \frac{\pi}{2}$. Each vector contains it's own displacement compared to before rotation.
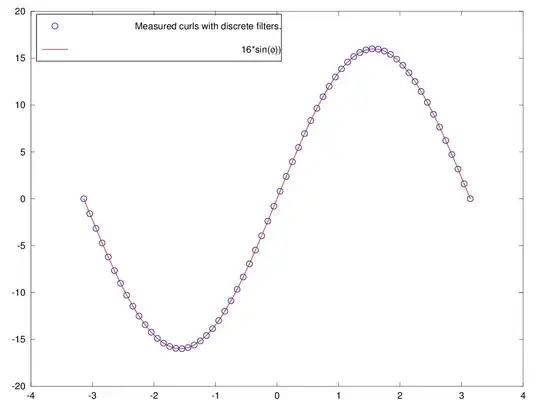
Applying the curl filters according to curl formula and fitting to a $sin$ curve shows that we can do curl on a proper rotation field and estimate phi., the scale 16 (sin maximum) can be adjusted by normalizing the discrete filters accordingly.
