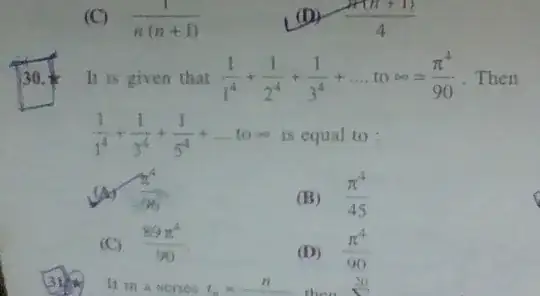I was doing my homework assignment and I did this question correctly. However, I'm interested in knowing the reason behind the logic that how $1/1^4 + 1/2^4 + 1/3^4$ .... to infinity evaluates to $pi^4/90$
Also, I know that whenever there is pi, somehow everything is related to circle. How is this question related to circle?
Here's a screenshot of my question if that helps! Thanks!