2

image of the triangle

AD, DE, EC and BC are equal in length, and the bottom two angles are the same. How can the exact value of angle BAC be found?

Waffle
  • 679

1 Answers1

3

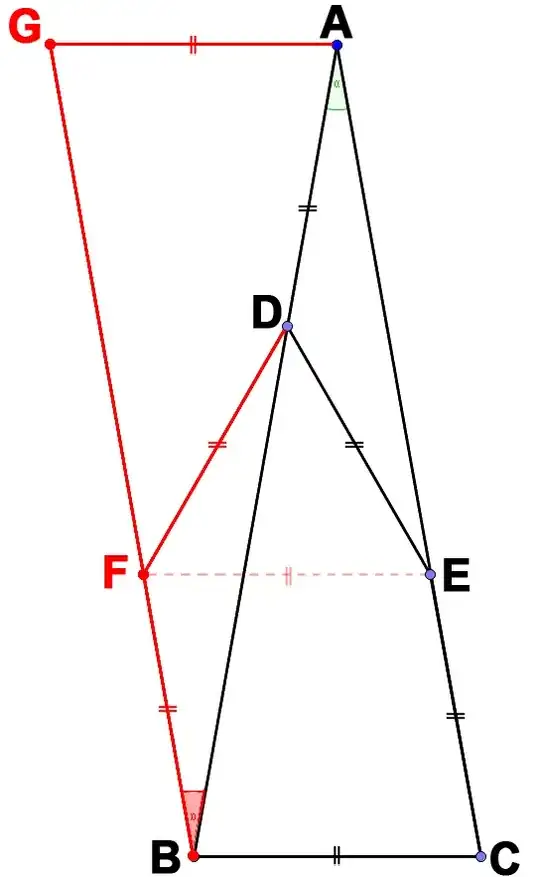
We construct new points $F$ and $G$ such that the configuration $ABCDE$ is congruent to the configuration $BGAFD$.

I will spoilerbox the rest of the proof as these new points give away most of the question.

More hints:

Note that $ACBG$ is a parallelogram and $FE$ is parallel and equal to $BC$. This creates the equilateral triangle $\triangle DEF$.

Rest of the question:

We can start chasing down angles. We have $\angle BCA=\angle FEA=60^\circ+\angle DEA=60^\circ+\angle BAC$ and $2\angle BCA=180^\circ-\angle BAC$. Solving, we have $\angle BAC=20^\circ$.

Picture (for a hint you might want to take a glance at this):

Piwi
  • 1,020
Element118
  • 3,753
  • 1
    I've taken the liberty to include a picture. The "congruent configuration" is achieved by mirroring horizontally and turning 180°. – Piwi Oct 10 '15 at 02:00
  • OK but how did you figure out what lines have to be added and where? I know many problems like this one, where drawing some additional lines at certain places makes the solution simple. But the hardest part for me is usually to figure out where those lines should be drawn in the first place. – BarbaraKwarc Aug 08 '16 at 21:19
  • @BarbaraKwarc The main motivation is to create equilateral triangles. Here, you notice that EC can be moved to AD to the newly created line DF to form an equilateral triangle. – Element118 Aug 09 '16 at 12:37