I have some interpretation of this fact, for $n = 3$ (and also other $n$ if you are willing to imagine $n$-cubes)
Because $f(x) = x^3 + a^3 = (x + a)(x + \zeta_3 a)(x + \zeta_3^2 a)$ we get that $a^3 + b^3 = (a+b)(\zeta_3 a+ b)(\zeta_3^2 a + b)$ where $\zeta_3 = -\frac{1}{2}-\frac{i \sqrt{3}}{2}$.
We can plot these in $\mathbb{C}$ in the following way:
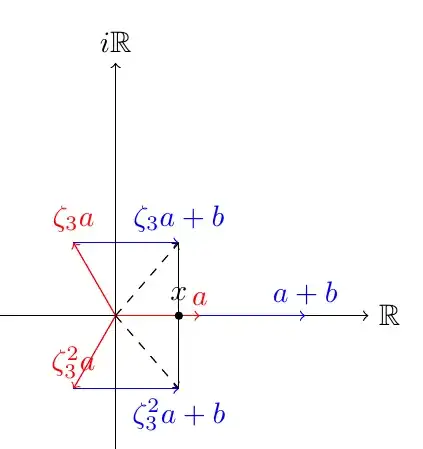
If we now rotate the vector $\zeta_3 a + b$ such that it aligns with the $i\mathbb{R}$ axis, and we rotate $\zeta_3^2 a + b$ such that it aligns with the axis perpendicular to the plane and then complete the cube, we get a cube with volume $a^3 + b^3$ with one rib being $a+b$.
It is possible to compute these rotated vectors, although too time consuming for me at this moment.
