15

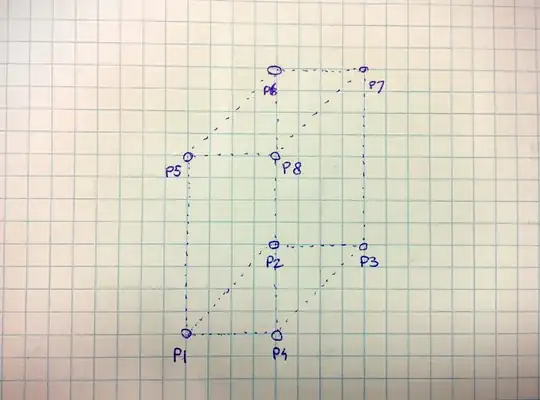
I am having a hard time figuring out if a 3D point lies in a cuboid (like the one in the picture below). I found a lot of examples to check if a point lies inside a rectangle in a 2D space for example this on but none for 3D space.

enter image description here

I have a cuboid in 3D space. This cuboid can be of any size and can have any rotation. I can calculate the vertices $P_1$ to $P_8$ of the cuboid.

Can anyone point me in a direction on how to determine if a point lies inside the cuboid?

Community
  • 1
Faas
  • 163

3 Answers3

19

The three important directions are $u=P_1-P_2$, $v=P_1-P_4$ and $w=P_1-P_5$. They are three perpendicular edges of the rectangular box.

A point $x$ lies within the box when the three following constraints are respected:

  • The dot product $u.x$ is between $u.P_1$ and $u.P_2$
  • The dot product $v.x$ is between $v.P_1$ and $v.P_4$
  • The dot product $w.x$ is between $w.P_1$ and $w.P_5$

EDIT:
If the edges are not perpendicular, you need vectors that are perpendicular to the faces of the box. Using the cross-product, you can obtain them easily:
$$u=(P_1-P_4)\times(P_1-P_5)\\ v=(P_1-P_2)\times(P_1-P_5)\\ w=(P_1-P_2)\times(P_1-P_4)$$ then check the dot-products as before.

Jealie
  • 103
Empy2
  • 50,853
  • In the case of perpendicular edges the constraints are that all the three dot products must be valid right not just any one of them? Superb answer by the way –  Sep 08 '18 at 10:10
  • 3
    According to my testing in unity, I had to check if ux is between uP2 & uP1; if vx is between vP4 & vP1; and if wx is between wP5 & wP1 (the inverse order) – Ugo Hed Dec 14 '19 at 19:11
  • @Empy2 do I need to normalize the direction vectors u,v,w ? – Kong Aug 09 '21 at 14:04
  • @Kong No, $ku.x$ is between $ku.P_1$ and $ku.P_2$ whenever $u.x$ is between $u.P_1$ and $u.P_2$ – Empy2 Aug 09 '21 at 14:26
  • Could somebody point me to a source for this? I see that it works, but I want to understand how, and I am not that much into geometry. – Valjean Jun 27 '22 at 13:21
  • for a non-math guy, are these p1 p2 etc the Position vectors of the co-ordinates ? How can i translate my x,y,z co-ordinate into these P1, P2 , etc ? – Aakash Uniyal Jul 25 '22 at 00:45
  • 1
    $P1=(x_1,y_1,z_1), P2=(x_2,y_2,z_2)$ and so on. – Empy2 Jul 25 '22 at 09:24
  • Can you please give some sources or explain, what is the reason behind these equations working the way they are working ? @Empy2 – Aakash Uniyal Aug 05 '22 at 07:55
  • @UgoHed is correct. This answer needs to be updated. – andre_ss6 Dec 28 '22 at 16:40
10

Given $p_1,p_2,p_4,p_5$ vertices of your cuboid, and $p_v$ the point to test for intersection with the cuboid, compute: $$\begin{matrix} i=p_2-p_1\\ j=p_4-p_1\\ k=p_5-p_1\\ v=p_v-p_1\\ \end{matrix}$$

then, if $$\begin{matrix} 0<v\cdot i<i\cdot i\\ 0<v\cdot j<j\cdot j\\ 0<v\cdot k<k\cdot k \end{matrix}$$ The point is within the cuboid.

Trey Reynolds
  • 628
  • I like this approach. Simple and clever. – Omid Jul 14 '22 at 15:25
  • for a non-math guy, are these p1 p2 etc the Position vectors of the co-ordinates ? How can i translate my x,y,z co-ordinate into these P1, P2 , etc ? – Aakash Uniyal Jul 25 '22 at 00:43
  • 1
    p1 is a vector which represents the position of the front bottom left point of the box. the front bottom left point of the box, p1, should have x y z coordinates. p1 = (x, y, z). You can perform b - a by doing (bx - ax, by - ay, bz - az). The dots represent dot product. a dot b = (ax, ay, az) dot (bx, by, bz) = axbx + ayby + az*bz – Trey Reynolds Jul 25 '22 at 04:36
  • @TreyReynolds thanks alot ! This helped :D – Aakash Uniyal Jul 25 '22 at 11:38
  • Can you please give some sources or explain, what is the reason behind these equations working the way they are working ? @TreyReynolds – Aakash Uniyal Aug 05 '22 at 08:05
0

Since 2-D problem is known, divide the problem into 3 parts.

Disregard z-coordinate. If any point is within box bounds $ x_2-x_1,y_2-y_1, $ select it and all other such points. Similarly y-z and z-x boxes.

Next choose points that the are common to three selections.

Narasimham
  • 40,495