2

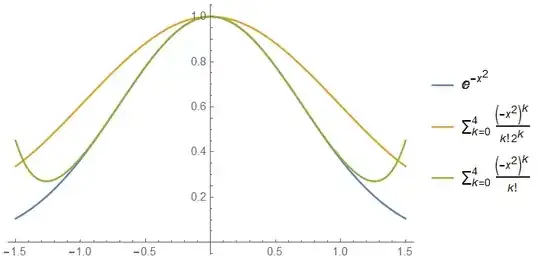
I was interested in one of the topics on this website, while I noticed a notation that I haven't been able to understand. This is the original question. One of the answers to the question states that $$ e^{-x^2}=1-(1/2)x^2+(1/2)(1/4)x^4-(1/6)(1/8)x^6+(1/24)(1/16)x^8+\cdots $$ I don't see how my answer would be different from his. Mine involved simply substituting $-x^{2}$ instead of the $x$ in the regular $e^{x}$'s expansion, yielding : $$ e^{-x^2}=1-x^2+(1/2)x^4-(1/6)x^6+(1/24)x^8+\cdots $$ Thanks for taking the time to read it through.

PS : I would have liked simply commenting on the answer to ask the original writer, but I apparently need a certain amount of "reputation" to do that.

Community
  • 1
Tasem
  • 29
  • 6
    the first equality is wrong. it looks like the expansion for $e^{-x^2/\textbf{2}}$ – tired Oct 05 '15 at 17:48
  • 3
    The original answer looks wrong to me. The Taylor polynomial of a function to order $n$ is unique, and yours is correct... – Chappers Oct 05 '15 at 17:48
  • Take some time to read the linked answer. It does state the mistake. My -1. –  Sep 17 '19 at 13:47

2 Answers2

1

Plotting the three functions show that you are correct. The first one would be a series of $e^{-x^2/2}$

Henricus V.
  • 18,694
-2

You can't put $-x^2$ at the place of x. Because the fact of the whole function will change because of the change of variable including the curvature. You have to use the theorem of Maclaurin. $f(x)= f(0) + xf'(0)/1! + x^2 f''(0)/2! + x^3 f'''(0)/3!+.............$

IamKnull
  • 1,497
  • 10
  • 29
lionel messi832
  • 1